Giải bài 10 tr 11 sách GK Toán 9 Tập 1
Chứng minh
a) \((\sqrt{3}- 1)^{2}= 4 - 2\sqrt{3}\) ; b) \(\sqrt{4 - 2\sqrt{3}}- \sqrt{3} = -1\)
Hướng dẫn giải chi tiết bài 10
Để chứng minh một biểu thức đại số bằng với một biểu thức đại số, ta sẽ biến đổi vế phải thành vế trái hoặc ngược lại. Cụ thể ở bài 10 này như sau:
Câu a:
\((\sqrt{3}- 1)^{2}= 4 - 2\sqrt{3}\)
Khai triển vế trái, ta được:
\((\sqrt{3}- 1)^{2}= (\sqrt{3})^2-2.\sqrt{3}.1+1^2=4-2\sqrt{3}=VP\)
Câu b:
Áp dụng kết quả nhận được từ câu a, ta chuyển vế thành:
\(\sqrt{4 - 2\sqrt{3}}= -1+\sqrt{3}\) ta vẫn sẽ có điều phải chứng minh. Tuy nhiên, các bạn có thể làm theo cách phân tích ngược lại như sau:
\(\sqrt{4-2\sqrt{3}}=\sqrt{3-2\sqrt{3}+1}=\sqrt{(\sqrt{3})^2-2.1.\sqrt{3}+1^2}=\sqrt{(\sqrt{3}-1)^2}\)
\(=|\sqrt{3}-1|=\sqrt{3}-1\) và ta có dpcm.
-- Mod Toán 9 HỌC247
-


Rút gọn biểu thức P(x)=1/căn x + căn x/ căn x + 1
bởi Nguyễn Thị Hà
 11/03/2020
11/03/2020
1/căn x + căn x/ căn x + 1
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình 1/x-1/y=1 và 2/x+4/y=5
bởi Nguyễn Thoa
 09/03/2020
09/03/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tính giá trị B=(√x+2)/(√x-5) khi x=64
bởi Momona Ichigo
 04/03/2020
04/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho điểm A nằm ngoài đường tròn (O;R). Vẽ tiếp tuyến AB của đường tròn (O) (B là iếp điểm). Kẻ day BC vuông góc với OA tại H. Chứng minh AC là tieps tuyến của đường tròn (O)
bởi Trang Anh
 29/02/2020
29/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải hệ phương trình 4x-2y=3 và 6x-3y=5
bởi Hương Giang Idol
 21/02/2020
Giúp tôi giat hệ phương trình và cách trình bày?
21/02/2020
Giúp tôi giat hệ phương trình và cách trình bày?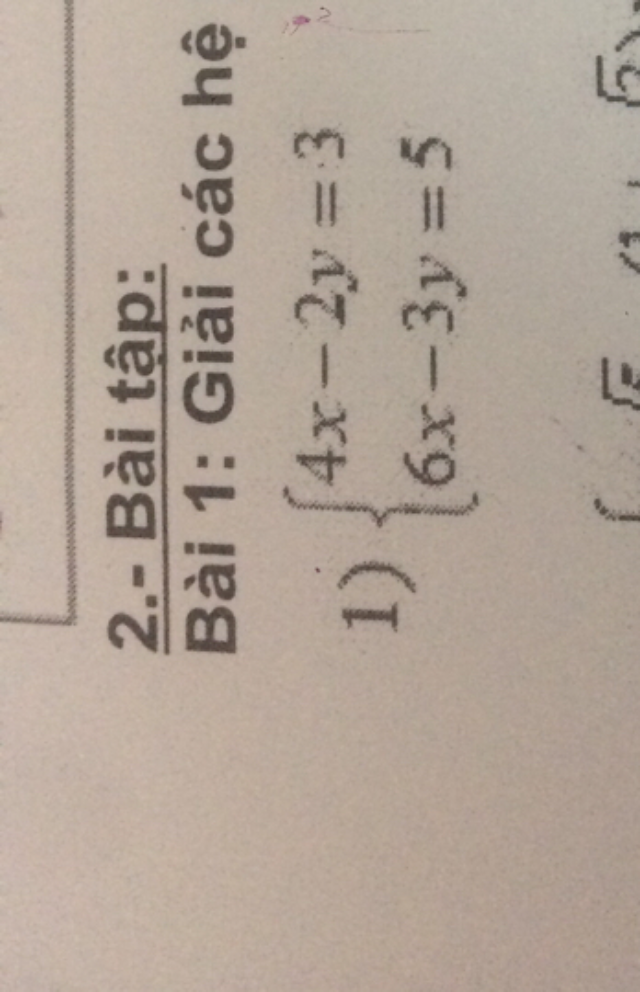 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Ttìm GTLN ,GTNN của biếu thức y=6-4x/x^2+1
bởi nhi đồng thị
 22/01/2020
22/01/2020
tìm GTLN ,GTNN của bt y=6-4x/x^2+1
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình căn(x^2-x+1/4)=2x^3-x^2+2x-1
bởi Lương Thùy Linh
 30/06/2019
30/06/2019
Giải phương trình sau:
Theo dõi (1) 3 Trả lời -


Chứng minh căn(1^3+2^3)=1+2
bởi Hồ Hà My
 16/06/2019
16/06/2019
Chung minh rang:
Theo dõi (1) 5 Trả lời -


Tìm số x không âm biết căn x=15
bởi vân anh
 13/11/2018
13/11/2018
ìm số x không âm, biết:
a) √x = 15; b) 2√x = 14
c) √x < √2; d) √2x < 4
Theo dõi (0) 2 Trả lời -


Chứng minh (3+căn 5)(căn 5-1)(căn(3-căn5))=4căn2
bởi hành thư
 14/09/2018
14/09/2018
(3+\(\sqrt{5}\))(\(\sqrt{5}\)-1)\(\sqrt{3-\sqrt{5}}\)=4\(\sqrt{2}\)
Chứng minh
Theo dõi (0) 1 Trả lời -


Giải phương trình 4/x + căn(x-1/x)=x+căn(2x-5/x)
bởi Sam sung
 03/01/2019
03/01/2019
giải pt :
a)\(\dfrac{4}{x}+\sqrt{x-\dfrac{1}{x}}=x+\sqrt{2x-\dfrac{5}{x}}\)
b) \(\sqrt{25-x^2}-\sqrt{9-x^2}=2\)
Theo dõi (0) 2 Trả lời -


Tìm điều kiện để các biểu thức có nghĩa và rút gọn chúng:
a) M = \(\sqrt{\dfrac{a^4b^3}{a^2b-ab}}\)
b) N = \(\dfrac{a}{b-1}.\sqrt{\dfrac{\left(b-1\right)^4}{a^2}}\)
Theo dõi (0) 2 Trả lời -


Tìm số nguyên m để căn (m^2+m+23) là số nguyên
bởi thu phương
 26/10/2018
26/10/2018
Tìm số nguyên m để \(\sqrt{m^2+m+23}\) là số nguyên.
Theo dõi (0) 2 Trả lời -


Tính T=x căn(1+y^2)+ y căn(1+x^2)
bởi Việt Long
 08/01/2019
08/01/2019
Cho \(x\times y+\sqrt{\left(1+x^2\right)\left(1+y^2\right)}=2018\) . Tính \(T=x\sqrt{1+y^2}+y\sqrt{1+x^2}\) .
Theo dõi (0) 3 Trả lời -


Tìm số nguyên x để A= căn x+3/căn x-2 là số nguyên
bởi bach dang
 26/10/2018
26/10/2018
Tìm \(x\in Z\) để \(A\in Z\) biết \(A=\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\) .
Theo dõi (0) 2 Trả lời -


Tìm GTLN của A= căn (3x-5)+căn(7-3x)
bởi het roi
 06/09/2018
06/09/2018
giá trị GTLN của biểu thức A = \(\sqrt{3x-5}+\sqrt{7-3x}\)
Theo dõi (0) 2 Trả lời -


Chứng minh số \(x=\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}+\dfrac{1}{\sqrt{100}}\) không phải là số tự nhiên.
Theo dõi (0) 2 Trả lời -


Tính 5+7 căn5/căn5 + 11 +căn11/1+căn11
bởi sap sua
 08/01/2019
08/01/2019
\(\dfrac{5+7\sqrt{5}}{\sqrt{5}}+\dfrac{11+\sqrt{11}}{1+\sqrt{11}}\)
Theo dõi (0) 2 Trả lời -


Tìm x biết x-(1/4 + 1/3) = -7/10
bởi Nhat nheo
 06/09/2018
06/09/2018
x-[1/4 + 1/3] = -7/10
Theo dõi (0) 1 Trả lời -


Tìm x để căn(x-2 căn(x-1)) có nghĩa
bởi Thanh Truc
 06/09/2018
06/09/2018
Với giá trị nào của x thì mỗi căn thức sau có nghĩa:
\(\sqrt{x-2\sqrt{x-1}}\)
Theo dõi (0) 2 Trả lời -


Tính 2 căn20 - căn50 + 3 căn80 - căn320
bởi truc lam
 08/01/2019
08/01/2019
\(a,2\sqrt{20}-\sqrt{50}+3\sqrt{80}-\sqrt{320}\)
\(b,\sqrt{32}-\sqrt{50}+\sqrt{18}\)
\(c,3\sqrt{3}+4\sqrt{2}-5\sqrt{27}\)
\(d,\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}-\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}+1}+1}\)
e,\(\left(2+\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\right)\left(2-\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\right)\)
Theo dõi (0) 2 Trả lời -


Tìm GTLN của P= căn(x-5)+căn(13-x)
bởi Anh Nguyễn
 08/01/2019
08/01/2019
Tìm GTLN của \(P=\sqrt{x-5}+\sqrt{13-x}\)
(Không dùng BĐT Caushy và BĐT Bunyakovsky)
Theo dõi (0) 2 Trả lời -


Tìm x để các căn thức có nghĩa (căn(x+2))/căn(x-1)
bởi Tuấn Huy
 09/01/2019
09/01/2019
Các bạn giúp mình bài này nhanh nhanh được không? Tại mình đang cần gấp
Tìm x để các căn thức sau có nghĩa :
a) (√x + 2)/ √(x-1)
b) √5 / 2x - 1
c) √(x - 2) / √(x +3)
d) 1/ 1 - √(x² - 3)
Các bạn giúp mình nhanh nhé. Mình cảm ơn nhiều
Theo dõi (0) 2 Trả lời -


Tính (căn2-căn7)-5căn(9+2căn14)
bởi My Hien
 14/09/2018
14/09/2018
\(\left(\sqrt{2}-\sqrt{7}\right)-5\sqrt{9+2\sqrt{14}}\)
Theo dõi (0) 2 Trả lời -


Tính 2 căn(15-căn216)+căn(33-12 căn6)
bởi Phạm Phú Lộc Nữ
 09/01/2019
09/01/2019
\(2\sqrt{15-\sqrt{216}}+\sqrt{33-12\sqrt{6}}\)
Theo dõi (0) 1 Trả lời -


Tính A= căn8-2căn15 -căn8+2căn15
bởi Sasu ka
 09/01/2019
09/01/2019
a, A= √8-2√15 -√8+2√15
b, B= √49+20√6 + √49-20√6
c, = √√5-√3-√29-12√5
d, √ x+2√x-1
Theo dõi (0) 1 Trả lời -


Rút gọn phép tính sau căn(5-2 căn6) - căn(4-2 căn 3)
bởi Thanh Truc
 07/01/2019
07/01/2019
rút gọn phép tính sau:
a) \(\sqrt{5-2\sqrt{6}}-\sqrt{4-2\sqrt{3}}\)
b) \(\sqrt{12+8\sqrt{2}+\sqrt{11-6\sqrt{2}}}\)
Theo dõi (0) 2 Trả lời -


Tính căn(11-x)+căn(x-5)
bởi Trần Bảo Việt
 09/01/2019
09/01/2019
a) \(\sqrt{11-x}+\sqrt{x-5}\)
b) \(\sqrt{x^2-2x+3}\)
c) \(\sqrt{2x-3}+\dfrac{1}{2x-5}\)
d)\(\sqrt{2-a}+\dfrac{1}{a}\)
2/tính
a) \(\sqrt{17-12\sqrt{2}}-2\sqrt{2}\)
b) \(\sqrt{15-6\sqrt{6}}+\sqrt{6}\)
Theo dõi (0) 1 Trả lời -


Tính 5/căn3 +2
bởi Nguyễn Thị Lưu
 09/01/2019
09/01/2019
\(\dfrac{5}{\sqrt{3}+2}\)
Theo dõi (0) 1 Trả lời -


Tính 2/căn10
bởi Phạm Hoàng Thị Trà Giang
 09/01/2019
09/01/2019
\(\dfrac{2}{\sqrt{10}}\)
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức A= căn(2+căn3)-căn(2-căn3)
bởi Nguyễn Minh Minh
 09/01/2019
09/01/2019
Rút gọn biểu thức sau:
A= \(\sqrt{2+\sqrt{3}}\) - \(\sqrt{2-\sqrt{3}}\)
Giúp mình với
Theo dõi (0) 1 Trả lời -


Tính căn(5+2 căn6 - căn(5-2 căn6))
bởi Hoa Lan
 09/01/2019
09/01/2019
\(\sqrt{5+2\sqrt{6}-\sqrt{5-2\sqrt{6}}}\)
Theo dõi (0) 1 Trả lời -


Tìm điều kiện có nghĩa của các căn thức sau:
a) \(\sqrt{3x-2}\) b) \(\sqrt{4-2x}\) c) \(\sqrt{-4x}\)
d)\(\sqrt{x^2-2x+1}\) e) \(\sqrt{\dfrac{x^2+1}{3-2x}}\) f) \(\sqrt{-15+8x-x^2}\)
Theo dõi (0) 1 Trả lời -


Tìm x biết căn(x-1)+1=x
bởi Nguyễn Lê Thảo Trang
 09/01/2019
09/01/2019
Tìm x:
a) \(\sqrt{x-1}+1=x\) b) \(\sqrt{9x^2}=2x+1\)
c) \(\sqrt{1-4x+x^2}=5\) d) \(\sqrt{2x-1}=x-2\)
Theo dõi (0) 1 Trả lời -


Tìm GTNN của M=căn(25x^2-20x +4)+căn25x^2
bởi Nguyễn Thị Lưu
 09/01/2019
09/01/2019
Tìm GTNN của \(M=\sqrt{25x^2-20x+4}+\sqrt{25x^2}\)
Theo dõi (0) 1 Trả lời -


Chứng minh căn(n+1)^2+căn(n^2)=(n+1)^2-n^2
bởi Nguyễn Minh Minh
 09/01/2019
09/01/2019
a) Với \(n\in N\). Chứng minh:
\(\sqrt{\left(n+1\right)^2}+\sqrt{n^2}=\left(n+1\right)^2-n^2\)
b) Cho a,b,c > 0. Chứng minh:
+) Nếu \(a+b+c=\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\) thì a = b = c.
+) \(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\ge\sqrt{\dfrac{a}{c}}+\sqrt{\dfrac{b}{a}}+\sqrt{\dfrac{c}{b}}\).
Theo dõi (0) 1 Trả lời -


Tính - căn7 =4
bởi Xuan Xuan
 09/01/2019
-\(\sqrt{7}\)=4Theo dõi (0) 1 Trả lời
09/01/2019
-\(\sqrt{7}\)=4Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức căn(a-5)^2 với a<=5
bởi hi hi
 09/01/2019
09/01/2019
Rút gọn biểu thức:
a)\(\sqrt{\left(a-5\right)^2}\) với \(a\le5\)
b)\(x-4+\sqrt{x^2-8x+16}\)với \(x< 4\)
c)\(\dfrac{3-\sqrt{x}}{x-9}\) (với \(x\ge0;x\ne9\))
Theo dõi (0) 1 Trả lời -


Tính căn(4x+1)+ căn(3x+4)=1
bởi Trần Thị Trang
 09/01/2019
09/01/2019
a)\(\sqrt{4x+1}+\sqrt{3x+4}=1\)
b)\(\sqrt{x-1}-\sqrt{x+1}=2\)
Theo dõi (0) 1 Trả lời -


Tính căn(x-1)+cănx +3+2 căn(x-1(x+3)=(4-2x)
bởi thu thủy
 10/01/2019
10/01/2019
\(\sqrt{x-1}+\sqrt{x}+3+2\sqrt{\left(x-1\left(x+3\right)\right)}=4-2x\)
Theo dõi (0) 1 Trả lời -


Tính căn(x-14)+căn12 - x =0
bởi Aser Aser
 10/01/2019
10/01/2019
\(\sqrt{x-14}+\sqrt{12}-x=0\)
Theo dõi (0) 1 Trả lời -


Tính x+cănx+1/cănx=3
bởi Nguyễn Minh Hải
 10/01/2019
10/01/2019
\(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}=3\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 8 trang 10 SGK Toán 9 Tập 1
Bài tập 9 trang 11 SGK Toán 9 Tập 1
Bài tập 11 trang 11 SGK Toán 9 Tập 1
Bài tập 12 trang 11 SGK Toán 9 Tập 1
Bài tập 13 trang 11 SGK Toán 9 Tập 1
Bài tập 14 trang 11 SGK Toán 9 Tập 1
Bài tập 15 trang 11 SGK Toán 9 Tập 1
Bài tập 16 trang 12 SGK Toán 9 Tập 1
Bài tập 12 trang 7 SBT Toán 9 Tập 1
Bài tập 13 trang 7 SBT Toán 9 Tập 1
Bài tập 14 trang 7 SBT Toán 9 Tập 1





