Bài tập 5 trang 10 SGK Giải tích 12

Phương pháp giải:

Với dạng bài tập ở bài 5 chứng minh \(g(x)>h(x)\) với x thuộc một miền cho trước ta thường tiến hành như sau:

Bước 1: \(g(x)>h(x)\Leftrightarrow g(x)-h(x)>0.\)

Bước 2: Đặt \(f(x)=h(x)-g(x)\), khảo sát tính đơn điệu của hàm số \(f(x)\).

Bước 3: Tìm x để \(f(x)=0\) (thường là hai đầu mút của miền đang xét). 

Bước 4: Từ tính đơn điệu của hàm số \(f(x)\) đưa ra kết luận cho bài toán.

Lời giải:

Ta áp dụng các bước trên để giải câu a, b bài 5:

Câu a:

Để chứng minh \(tanx >x\) với mọi \(0 < x < \frac{\pi }{2}\) ta chứng minh tanx - x > 0 với mọi \(0 < x < \frac{\pi }{2}\) 

Trước tiên ta cần kiểm tra xem có tồn tại giá trị nào của x đề tanx-x=0 hay không, mà trước hết ta cần thử với hai giá trị là x=0 và \(x=\frac{\pi}{2}.\)

Dễ thấy: \(tan(0)-0=0.\)

Khi đó ta tiến hành mở rộng khoảng đang xét thành nửa khoảng, cụ thể lời giải chi tiết như sau:

Xét hàm số f(x)= tanx–x liên tục trên nửa khoảng \(\left [0;\frac{\pi}{2} \right )\)

\(f'(x) = \frac{1}{{{{\cos }^2}x}} - 1 > 0\) với mọi \(x\in\left ( 0;\frac{\pi}{2} \right )\).

\(f'(x)=0\Leftrightarrow x=0.\)

Bảng biến thiên:

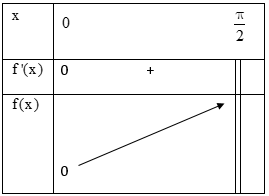
Vậy hàm số đồng biến trên \(\left [0;\frac{\pi}{2} \right )\).

Vậy với \(0 < x < \frac{\pi }{2}\) ta có \(f\left( x \right) > f\left( 0 \right) = 0 \Rightarrow tanx > x\) với mọi \(x\in\left ( 0;\frac{\pi}{2} \right )\).

Câu b:

Chứng minh \(\tan x > x +\frac{x^3}{3} (0 < x < \frac{\pi }{2})\)

Tương tự câu a.

Xét hàm số \(g(x) = \tan x - x - \frac{{{x^3}}}{3}\) liên tục trên \(\left[ {0;\frac{\pi }{2}} \right)\) có đạo hàm:

\(g'(x) = \frac{1}{{{{\cos }^2}x}} - 1 - {x^2} = {\tan ^2}x - {x^2}\)

\(= (tanx - x)(tanx + x) > 0,\,\forall x \in \left( {0;\frac{\pi }{2}} \right)\)  (Theo câu a)

\(g'(x)=0\Leftrightarrow x=0.\)

Bảng biến thiên:

Vậy hàm số đồng biến trên \(\left[ {0;\frac{\pi }{2}} \right)\).

Vậy với \(0 < x < \frac{\pi }{2}\) ta có \(g\left( x \right) > g\left( 0 \right) \Rightarrow tanx > x + \frac{{{x^3}}}{3}\) với mọi \(x\in\left ( 0;\frac{\pi}{2} \right )\).

Nhận xét:

Với dạng bài tập chứng minh f(x)>0 với x thuộc khoảng (a;b). Nếu f(a) và f(b) đề khác không, hoặc f(x) không xác định tại a và b. Thì f(x)=0 tại x₀, với x₀ là nghiệm của phương trình f'(x)=0, ta không cần mở rộng khoảng đang xét.

-- Mod Toán 12 HỌC247