Toán 12 Ôn tập chương 3 Nguyên hàm, Tích phân và Ứng dụng

Lý thuyết10 Trắc nghiệm58 BT SGK 379 FAQ

Bài ôn tập chương Nguyên hàm - Tích phân và ứng dụng sẽ giúp các em hệ thống lại kiến thức của toàn bộ các bài đã học thông qua các sơ đồ, cùng với đó là các bảng tra cứu nhanh nguyên hàm các hàm số quen thuộc,...sẽ giúp các em ghi nhớ bài học tốt hơn.

YOMEDIA

1. Video bài giảng

2. Tóm tắt lý thuyết

2.1. Sơ đồ chung các bài toán tích phân và ứng dụng

2.2. Bảng công thức nguyên hàm của một số hàm số

2.3. Dạng nguyên hàm từng phần và cách chọn u, dv

2.4. Dạng nguyên hàm vô tỉ

3. Bài tập minh hoạ

4. Luyện tập Ôn tập Chương 3 Toán 12

4.1. Trắc nghiệm

4.2. Bài tập SGK

5. Hỏi đáp Ôn tập Chương 3 Toán 12

Tóm tắt lý thuyết

2.1. Sơ đồ chung các bài toán tích phân và ứng dụng

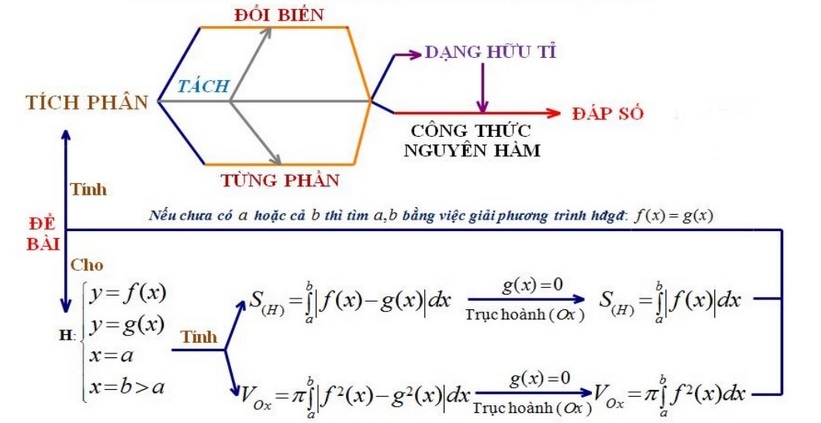
Sơ đồ tư duy các bài toán tích phân

2.2. Bảng công thức nguyên hàm của một số hàm số

Bảng công thức nguyên hàm của một số hàm số

2.3. Các dạng nguyên hàm từng phần và cách chọn u, dv

Các dạng nguyên hàm từng phần và cách chọn u, dv

2.4. Các dạng nguyên hàm vô tỉ và các phép đổi biến số lượng giác hóa

Các dạng nguyên hàm vô tỉ và các phương pháp đổi biến số lượng giác hóa

Bài tập minh họa

Bài tập 1:

Tìm các nguyên hàm sau:

a) \(I = \int\limits {\left( {3x + 1} \right)\left( {x - 2} \right)} \,dx\).

b) \(J = \int\limits {\left( {5{{\sin }^2}x - \sin x + 2} \right)\cos x} \,dx\).

Lời giải:

a) \(I = \int\limits {\left( {3x + 1} \right)\left( {x - 2} \right)} \,dx\)

\(I = \int\limits {\left( {3{x^2} - 5x - 2} \right)} \,dx = {x^3} - \frac{{5{x^2}}}{2} - 2x + C.\)

b) \(J = \int\limits {\left( {5{{\sin }^2}x - \sin x + 2} \right)\cos x} \,dx\)

Đặt: \(t = \sin x \Rightarrow dt = \cos xdx\)

Khi đó: \(J = \int\limits {\left( {5{t^2} - t + 2} \right)} \,dt = \frac{{5{t^3}}}{3} - \frac{{{t^2}}}{2} + 2t + C = \frac{5}{3}{\sin ^3}x - \frac{{{{\sin }^2}x}}{2} + 2\sin x + C.\)

Bài tập 2:

Tính các tích phân sau:

a) \(I=\int_{1}^{3}x(3x+2lnx)dx.\)

b) \(I=\int_{1}^{2}\frac{x^2+ln^2x}{x}dx.\)

c) \(I = \int\limits_{\frac{{\sqrt 2 }}{2}}^1 {\frac{{\sqrt {1 - {x^2}} }}{{{x^2}}}dx} .\)

Lời giải:

a) \(I=\int_{1}^{2}3x^2dx+\int_{1}^{2}2xlnxdx\)
Đặt \(I_1=\int_{1}^{2}3x^2dx; I_2=\int_{1}^{2}2xlnxdx\)
\(I_1=\int_{1}^{2}3x^2dx=x^3\bigg |^2_1=7.\)
\(I_2=\int_{1}^{2}lnxd(x^2)=(x^2lnx)\bigg|^2_1-\int_{1}^{2}xdx=4ln2- \frac{x^2}{2}\bigg|^2_1=4ln2-\frac{3}{2}.\)
Vậy \(I=I_1+I_2=4ln2-\frac{11}{2}.\)

b) Ta tách tích phân I như sau: \(I=\int_{1}^{2}\frac{x^2+ln^2x}{x}dx=\int_{1}^{2}xdx+\int_{1}^{2}\frac{ln^2x}{x}dx\)
\(I_1=\int_{1}^{2}xdx=\frac{x^2}{2}\bigg|^2_1=\frac{3}{2}\)
\(I_2=\int_{1}^{2}\frac{ln^2x}{x}dx\)
Đặt \(t=lnx\Rightarrow dt=\frac{1}{x}dx\)
Đổi cận: \(x=2\Rightarrow t=ln2;x=1\Rightarrow t=0\)
\(I_2=\int_{0}^{ln2}t^2dt=\frac{t^3}{3}\bigg |^{ln2}_0=\frac{ln^32}{3}\)
Vậy \(I=I_1+I_2=\frac{3}{2}+\frac{ln^32}{3}.\)

c) \(I = \int\limits_{\frac{{\sqrt 2 }}{2}}^1 {\frac{{\sqrt {1 - {x^2}} }}{{{x^2}}}dx} .\)

Đặt \(x = \cos t,t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow dx = - \sin tdt\)

Đổi cận: \(\left\{ \begin{array}{l} x = \frac{{\sqrt 2 }}{2} \Rightarrow t = \frac{\pi }{4}\\ x = 1 \Rightarrow t = 0 \end{array} \right.\)

Khi đó:

\(\begin{array}{l} I = - \int\limits_{\frac{\pi }{4}}^0 {\frac{{\sqrt {1 - {{\cos }^2}t} .\sin t}}{{{{\cos }^2}t}}dt} = \int\limits_0^{\frac{\pi }{4}} {\frac{{\left| {\sin t} \right|.\sin t}}{{{{\cos }^2}t}}dt} \\ = \int\limits_0^{\frac{\pi }{4}} {\left( {\frac{1}{{{{\cos }^2}t}} - 1} \right)dt} = \left. {\left( {\tan t - t} \right)} \right|_0^{\frac{\pi }{4}} = 1 - \frac{\pi }{4}. \end{array}\)

Bài tập 3:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x2 + x, trục hoành và hai đường thẳng x = 0, x = 1.

Lời giải:

Diện tích hình phẳng cần tính là: \(S=\int_{0}^{1}\left | x^2+x \right |dx\)
Với \(x\in [0;1]\Rightarrow S=\int_{0}^{1}(x^2+x)dx\)
Suy ra \(S=(\frac{x^3}{3}+\frac{x^2}{2})\bigg |^1_0=\frac{5}{6}.\)
Vậy \(S=\frac{5}{6}\).

Bài tập 4:

Cho hình phẳng giới hạn bởi các đường \(y = \frac{1}{{1 + \sqrt {4 - 3{\rm{x}}} }},y = 0,x = 0,x = 1\) quay quanh trục Ox. Tính thể tích V của khối tròn xoay tạo thành.

Lời giải:

Thể tích cần tìm: \(V = \pi \int\limits_0^1 {\frac{{dx}}{{{{\left( {1 + \sqrt {4 - 3x} } \right)}^2}}}}\)

Đặt:\(t = \sqrt {4 - 3x} \Rightarrow dt = - \frac{3}{{2\sqrt {4 - 3x} }}dx \Leftrightarrow dx = - \frac{2}{3}tdt\left( {x = 0 \Rightarrow t = 2;x = 1 \Rightarrow t = 1} \right)\)

Khi đó:

\(\begin{array}{l} V = \frac{{2\pi }}{3}\int\limits_1^2 {\frac{t}{{{{\left( {1 + t} \right)}^2}}}dt} = \frac{{2\pi }}{3}\int\limits_1^2 {\left( {\frac{1}{{1 + t}} - \frac{1}{{{{\left( {1 + t} \right)}^2}}}} \right)dt} \\ = \left. {\frac{{2\pi }}{3}\left( {\ln \left| {1 + t} \right| + \frac{1}{{1 + t}}} \right)} \right|_1^2 = \frac{\pi }{9}\left( {6\ln \frac{3}{2} - 1} \right). \end{array}\)

4. Luyện tập Ôn tập Chương 3 Toán 12

4.1 Trắc nghiệm

Để cùng cố bài học xin mời các em củng làm Bài kiểm tra Trắc nghiệm Toán 12 Ôn tập chương 3 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Hàm số nào sau đây không phải làm nguyên hàm của hàm số \(f(x) = 2\sin 2x.\)
- A. \(F(x) = 2{\sin ^2}x\)
- B. \(F(x) = - 2{\cos ^2}x\)
- C. \(F(x) = - 1 - \cos 2x\)
- D. \(F(x) = - 1 - 2\cos x\sin x\)
Câu 2:
Biết \(F\left( x \right) = \left( {ax + b} \right).{e^x}\) là nguyên hàm của hàm số \(y = \left( {2x + 3} \right).{e^x}.\) Tính tổng a + b.
- A. a+b=2
- B. a+b=3
- C. a+b=4
- D. a+b=5
Câu 3:
Trong các tích phân sau, tích phân nào không có cùng giá trị với \(I = \int\limits_1^2 {{x^3}\sqrt {{x^2} - 1} dx} .\)
- A. \(\frac{1}{2}\int_1^2 {t\sqrt {t - 1} dt}\)
- B. \(\frac{1}{2}\int_1^4 {t\sqrt {t - 1} dt}\)
- C. \(\int_0^{\sqrt 3 } {\left( {{t^2} + 1} \right){t^2}dt}\)
- D. \(\int_0^{\sqrt 3 } {\left( {{x^2} + 1} \right){x^2}dx}\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

4.2 Bài tập SGK

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 12 Ôn tập chương 3 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Giải tích 12 Cơ bản và Nâng cao.

Bài tập 1 trang 126 SGK Giải tích 12

Bài tập 2 trang 126 SGK Giải tích 12

Bài tập 3 trang 126 SGK Giải tích 12

Bài tập 4 trang 126 SGK Giải tích 12

Bài tập 5 trang 127 SGK Giải tích 12

Bài tập 6 trang 127 SGK Giải tích 12

Bài tập 7 trang 127 SGK Giải tích 12

Bài tập 1 trang 128 SGK Giải tích 12

Bài tập 2 trang 128 SGK Giải tích 12

Bài tập 3 trang 128 SGK Giải tích 12

Bài tập 4 trang 128 SGK Giải tích 12

Bài tập 5 trang 128 SGK Giải tích 12