Bài tập 49 trang 176 SGK Toán 12 NC
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. biết rằng B đuổi kịp A sau 8 giây ( kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
Hướng dẫn giải chi tiết
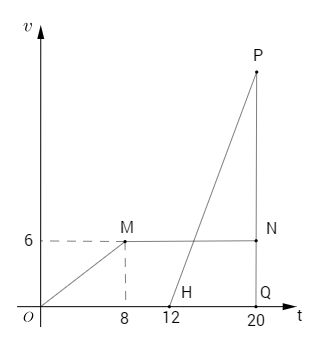
Thời điểm A và B gặp nhau là 20 giây kể từ lúc A xuất phát. Đồ thị của vận tốc của A là đường gấp khúc OMN.
Quãng đường mà A đi được (s = v.t) là diện tích hình thang OMNQ.
\({S_{OMNQ}} = \frac{1}{2}(20 + 12).6 = 96\)
Vậy lúc gặp B, A đi được 96m.
Đồ thị vận tốc của B là đường thẳng HP. Vì B xuất phát cùng vị trí với A nên B cũng đi được 96m. Quãng đường B đi được bằng diện tích tam giác HPQ.
Ta có:
\(\begin{array}{l}
{S_{HPQ}} = \frac{1}{2}.PQ.HQ\\
\Rightarrow 96 = \frac{1}{2}PQ.8 \Rightarrow PQ = 24.
\end{array}\)
Vậy vận tốc của B tại thời điểm gặp A là 24m/s.
-- Mod Toán 12 HỌC247
-


Cho F(x) là nguyên hàm của hàm số \(f(x) = \dfrac{1}{{x - 1}}\,,\,\,F(2) = 1\). Cho biết F(3) bằng bao nhiêu?
bởi Lê Trung Phuong
 06/05/2021
06/05/2021
A. \(F(3) = \dfrac{1}{2}\).
B. \(F(3) = \ln \dfrac{3}{2}\).
C. F(3) = ln2.
D. F(3) = ln2 + 1.
Theo dõi (0) 1 Trả lời -


Ta cho F(x) là một nguyên hàm của hàm số \(f(x) = {e^x} + 2x\) thỏa mãn \(F(0) = \dfrac{3}{2}\). Hãy tìm F(x)?
bởi Cam Ngan
 05/05/2021
05/05/2021
A. \(F(x) = {e^x} + {x^2} + \dfrac{3}{2}\).
B. \(F(x) = {e^x} + {x^2} + \dfrac{5}{2}\).
C. \(F(x) = {e^x} + {x^2} + \dfrac{1}{2}\).
D. \(F(x) = 2{e^x} + {x^2} - \dfrac{1}{2}\).
Theo dõi (0) 1 Trả lời -


Các hàm số f(x) dưới đây. Cho biết hàm số nào thỏa mãn đẳng thức \(\int {f(x).\sin x\,dx = - f(x).\cos x + \int {{\pi ^x}.\cos x\,dx} } \)?
bởi Bao Nhi
 06/05/2021
06/05/2021
A. \(f(x) = {\pi ^x}\ln x\).
B. \(f(x0 = - {\pi ^x}\ln x\).
C. \(f(x) = \dfrac{{{\pi ^x}}}{{\ln \pi }}\).
D. \(f(x) = \dfrac{{{\pi ^x}}}{{\ln x}}\).
Theo dõi (0) 1 Trả lời -


Tích phân su: \(\int\limits_0^1 {x\sqrt {{x^2} + 1} } dx = \dfrac{{a\sqrt 2 - b}}{3}\) thì a + b bằng bao nhiêu?
bởi bach hao
 05/05/2021
05/05/2021
A. 2
B. 4
C. 3
D. 5
Theo dõi (0) 1 Trả lời -


Tính tích phân sau: \(\int\limits_a^{\dfrac{\pi }{2} - a} {{\sin }^2}x\,dx;\,\,\dfrac{\pi }{2} > a > 0 \).
bởi Lê Nhật Minh
 06/05/2021
06/05/2021
A. \( - \dfrac{1}{4}\sin \left( {\pi - 2a} \right) - \sin 2a + \pi - 4a\).
B. \( \dfrac{1}{4}\left( {\sin \left( {\pi - 2a} \right) - \sin 2a + \pi - 4a} \right)\).
C. \( - \dfrac{1}{4}\left( {\sin \left( {\pi - 2a} \right) - \sin 2a + \pi - 4a} \right)\).
D. 0.
Theo dõi (0) 1 Trả lời -


Diện tích hình phẳng giới hạn bởi các đường : \(y = {x^2}\,,\,y = \dfrac{{{x^2}}}{8},\,\,y = \dfrac{{27}}{x}\) là bằng bao nhiêu?
bởi Goc pho
 06/05/2021
06/05/2021
A. 27ln2.
B. 72ln27
C. 3ln72.
D. Một kết quả khác.
Theo dõi (0) 1 Trả lời -


Cho \(f(x) \ge g(x),\forall x \in [a;b]\). Hình phẳng S1 giới hạn bởi đường y = f(x), y = 0, x = a, x = b (a
bởi Nguyễn Hoài Thương
 06/05/2021
06/05/2021
A. Nếu V1 = V2 thì chắc chắn suy ra \(f(x) = g(x),\forall x \in [a;b]\).
B. S1>S2.
C. V1 > V2.
D. Cả 3 phương án trên đều sai.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 47 trang 176 SGK Toán 12 NC
Bài tập 48 trang 176 SGK Toán 12 NC
Bài tập 50 trang 176 SGK Toán 12 NC
Bài tập 51 trang 176 SGK Toán 12 NC
Bài tập 52 trang 177 SGK Toán 12 NC
Bài tập 53 trang 177 SGK Toán 12 NC
Bài tập 54 trang 177 SGK Toán 12 NC
Bài tập 55 trang 177 SGK Toán 12 NC
Bài tập 56 trang 177 SGK Toán 12 NC
Bài tập 57 trang 177 SGK Toán 12 NC
Bài tập 58 trang 177 SGK Toán 12 NC
Bài tập 59 trang 177 SGK Toán 12 NC
Bài tập 60 trang 178 SGK Toán 12 NC
Bài tập 61 trang 178 SGK Toán 12 NC
Bài tập 62 trang 178 SGK Toán 12 NC
Bài tập 63 trang 178 SGK Toán 12 NC
Bài tập 64 trang 178 SGK Toán 12 NC
Bài tập 65 trang 178 SGK Toán 12 NC
Bài tập 66 trang 179 SGK Toán 12 NC
Bài tập 67 trang 179 SGK Toán 12 NC
Bài tập 3.43 trang 180 SBT Toán 12
Bài tập 3.44 trang 180 SBT Toán 12
Bài tập 3.45 trang 181 SBT Toán 12
Bài tập 3.46 trang 181 SBT Toán 12
Bài tập 3.47 trang 181 SBT Toán 12
Bài tập 3.48 trang 181 SBT Toán 12
Bài tập 3.49 trang 182 SBT Toán 12
Bài tập 3.50 trang 182 SBT Toán 12
Bài tập 3.51 trang 182 SBT Toán 12
Bài tập 3.52 trang 182 SBT Toán 12
Bài tập 3.53 trang 183 SBT Toán 12
Bài tập 3.54 trang 183 SBT Toán 12
Bài tập 3.55 trang 183 SBT Toán 12
Bài tập 3.56 trang 183 SBT Toán 12
Bài tập 3.67 trang 183 SBT Toán 12
Bài tập 3.58 trang 184 SBT Toán 12





