Bài tập 3.52 trang 182 SBT Toán 12
Tìm khẳng định đúng trong các khẳng định sau:
A. \(\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = \int \limits_0^\pi \left| {\sin \left( {x - \frac{\pi }{4}} \right)} \right|dx\)
B. \(\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = \int \limits_0^\pi \left| {\cos \left( {x + \frac{\pi }{4}} \right)} \right|dx\)
C. \(\begin{array}{l}
\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx\\
= \int \limits_0^{\frac{{3\pi }}{4}} \sin \left( {x + \frac{\pi }{4}} \right)dx - \int \limits_{\frac{{3\pi }}{4}}^\pi \sin \left( {x + \frac{\pi }{4}} \right)dx
\end{array}\)
D. \(\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = 2\int \limits_0^{\frac{\pi }{4}} \sin \left( {x + \frac{\pi }{4}} \right)dx\)
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{l}
\sin \left( {x + \frac{\pi }{4}} \right) \ge 0\\
\Leftrightarrow 0 \le x + \frac{\pi }{4} \le \pi \\
\Leftrightarrow - \frac{\pi }{4} \le x \le \frac{{3\pi }}{4}
\end{array}\)
\(\begin{array}{l}
\sin \left( {x + \frac{\pi }{4}} \right) < 0 \Leftrightarrow \pi < x + \frac{\pi }{4} < 2\pi \\
\Leftrightarrow \frac{{3\pi }}{4} < x < \frac{{7\pi }}{4}
\end{array}\)
Khi đó \(\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx\)
\( = \int \limits_0^{\frac{{3\pi }}{4}} \sin \left( {x + \frac{\pi }{4}} \right)dx - \int \limits_{\frac{{3\pi }}{4}}^\pi \sin \left( {x + \frac{\pi }{4}} \right)dx\)
Chọn C.
-- Mod Toán 12 HỌC247
-


Tính giá trị của biểu thức S=f(-ln16)+ f(ln4)
bởi Nguyễn Diệu Thu
 09/02/2020
Cho hàm số f(x) xác định trẻn R thoả mãn f'(x)=√e^(x) e^(-x)-2 ,f(0)=5 và f(ln(1/4))=0. Giá trị của biểu thức S=f(-ln16) f(ln4) bằng:Theo dõi (1) 3 Trả lời
09/02/2020
Cho hàm số f(x) xác định trẻn R thoả mãn f'(x)=√e^(x) e^(-x)-2 ,f(0)=5 và f(ln(1/4))=0. Giá trị của biểu thức S=f(-ln16) f(ln4) bằng:Theo dõi (1) 3 Trả lời -


Tìm nguyên hàm của x/cos^2 x?
bởi Nhất Phi
 07/02/2020
07/02/2020
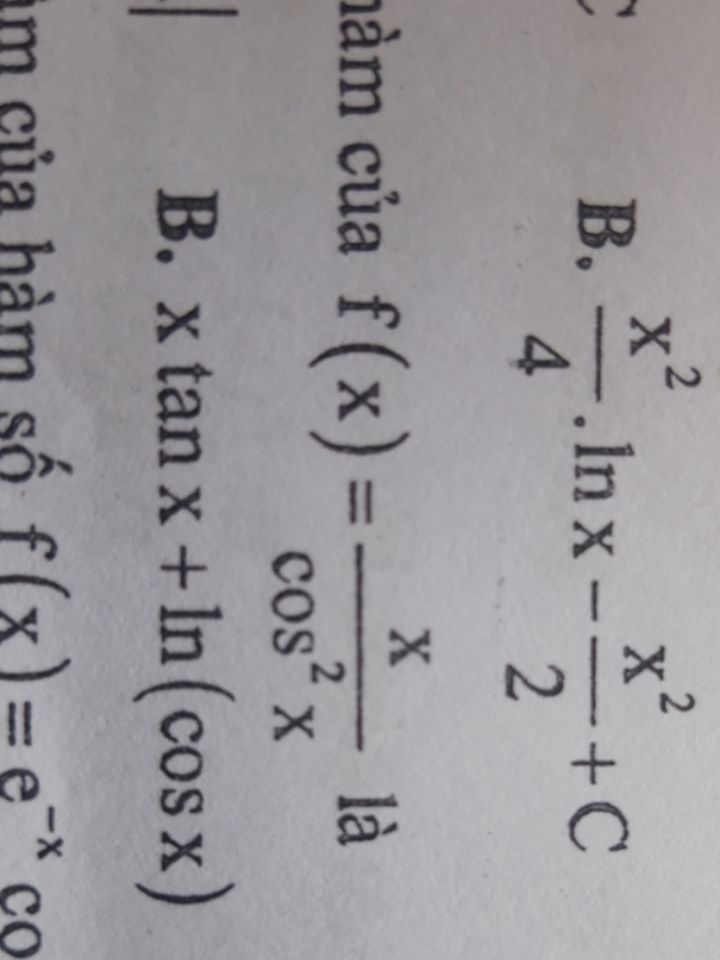 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Khi S1=S2 thì a thuộc khoảng nào biết S1, S2 là diện tích của hai hình phẳng được gạch chéo?
bởi Nguyễn Nhi
 05/02/2020
giải bài tập
05/02/2020
giải bài tập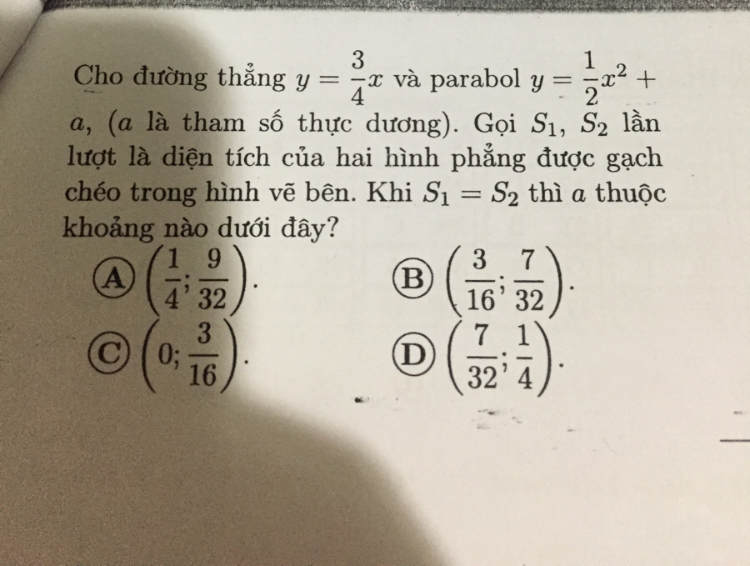 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y=f(x), trục hoành và hai đường thẳng x=1, x=4
bởi Thilam Nguyen
 30/01/2020
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [1,4] thỏa mãn f(1)=2 và 2xf'(x)-f(x) = 3x^2, mọi x thuộc [1,4]. Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y=f(x), trục hoành và hai đường thẳng x=1, x=4Theo dõi (0) 0 Trả lời
30/01/2020
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [1,4] thỏa mãn f(1)=2 và 2xf'(x)-f(x) = 3x^2, mọi x thuộc [1,4]. Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y=f(x), trục hoành và hai đường thẳng x=1, x=4Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm e^(x^2)
bởi Phạm Khánh Linh
 27/01/2020
Nguyên hàm e^(x^2)Theo dõi (0) 0 Trả lời
27/01/2020
Nguyên hàm e^(x^2)Theo dõi (0) 0 Trả lời -


Tính giá trị biểu thức P=2a^2+3b biết tích phân từ 1 đến 4 của (4x-5)/(x^2-x-2)dx=aln5+bln2
bởi Nguyễn Hoài Vy
 17/01/2020
Giải câu 7,8 giúp mình với ạ
17/01/2020
Giải câu 7,8 giúp mình với ạ Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tính diện tích hình phẳng giới hạn bởi y=2x+1/x-2
bởi Bùi Thúy Hằng
 12/01/2020
12/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.50 trang 182 SBT Toán 12
Bài tập 3.51 trang 182 SBT Toán 12
Bài tập 3.53 trang 183 SBT Toán 12
Bài tập 3.54 trang 183 SBT Toán 12
Bài tập 3.55 trang 183 SBT Toán 12
Bài tập 3.56 trang 183 SBT Toán 12
Bài tập 3.67 trang 183 SBT Toán 12
Bài tập 3.58 trang 184 SBT Toán 12





