Hướng dẫn Giải bài tập Toán 12 Ôn tập chương 3 Nguyên hàm, Tích phân và Ứng dụng sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức đã học.
-
Bài tập 1 trang 126 SGK Giải tích 12
a) Phát biểu định nghĩa nguyên hàm của hàm số f(x) trên một khoảng.
b) Nêu phương pháp tính nguyên hàm từng phần. Cho ví dụ minh họa.
-
Bài tập 2 trang 126 SGK Giải tích 12
a) Phát biểu định nghĩa tích phân của hàm số f(x) trên một đoạn.
b) Nêu các tính chất của tích phân. Cho ví dụ minh họa.
-
Bài tập 3 trang 126 SGK Giải tích 12
Tìm nguyên hàm của các hàm số sau:
a) \(f(x)=(x-1)(1-2x)(1-3x)\)
b) \(f(x)=sin4xcos^22x\)
c) \(f(x)=\frac{1}{1-x^2}\)c)\(f(x)=(e^x-1)^3\)
-
Bài tập 4 trang 126 SGK Giải tích 12
Tính:
a) \(\int (2-x)sinxdx\)
b) \(\frac{\int (x+1)^2}{\sqrt{x}}dx\)
c) \(\int \frac{e^{3x+1}}{e^x+1}dx\)
d) \(\int \frac{1}{(sinx+cosx)^2}dx\)
e) \(\int \frac{1}{\sqrt{1+x}+\sqrt{x}}dx\)
f) \(\int \frac{1}{(1+x)(2-x)}dx\) -
Bài tập 5 trang 127 SGK Giải tích 12
Tính:
a) \(\int_{3}^{0}\frac{x}{\sqrt{1+x}}dx\)
b) \(\int_{1}^{64} \frac{1+\sqrt{x}}{\sqrt[3]{x}}dx\)
c) \(\int_{0}^{2} x^2.e^{3x}dx\)
d) \(\int_{0}^{\pi} \sqrt{1+sin2x}dx\) -
Bài tập 6 trang 127 SGK Giải tích 12
Tính:
a) \(\int_{0}^{\frac{\pi}{2}}cos2xsin^2xdx\)
b) \(\int_{-1}^{1}\left | 2^2-2^{-x} \right |dx\)
c) \(\int_{-1}^{2} \frac{(x+1)(x+2)(x+3)}{x^2}dx\)
d) \(\int_{-1}^{\frac{\pi }{2}} (sinx+cosx)^2dx\)
e) \(\int_{-1}^{\pi } (x+sinx)^2dx\)
g) \(\int_{0}^{\pi }(x+sinx)^2dx\)
-
Bài tập 7 trang 127 SGK Giải tích 12
Xét hình phẳng D giới hạn bởi \(y=2\sqrt{1-x^2}\) và \(y=2(1-x)\)
a) Tính diện tích hình D
b) Quay hình D xung quanh trục Ox. Tính thể tích khối tròn xoay được tạo thành.
-
Bài tập 1 trang 128 SGK Giải tích 12
Tính \(\frac{\int dx}{\sqrt{1-x}}\) kết quả:
(A). \(\frac{C}{ \sqrt{1-x}}\) (B) \(C\sqrt{1-x}\)
(C). \(-2\sqrt{1-x}+C\) (D) \(\frac{2}{\sqrt{1-x}}+C\)
-
Bài tập 2 trang 128 SGK Giải tích 12
Tính \(\int 2^{\sqrt{x}}.\frac{ln2}{\sqrt{x}}dx\), kết quả sai là:
(A) \(2^{\sqrt{x}+1}+C\)(B) \(2(2^{\sqrt{x}}-1)+C\)
(C) \(2(2^{\sqrt{x}}+1)+C\)
(D) \(2^{\sqrt{x}}+C\)
-
Bài tập 3 trang 128 SGK Giải tích 12
Tích phân \(\int_{0}^{\pi}cos^2x sinxdx\) bằng:
(A) \(-\frac{2}{3}\) (B) \(\frac{2}{3}\)(C) \(\frac{3}{2}\) (D) 0
-
Bài tập 4 trang 128 SGK Giải tích 12
Cho hai tích phân \(\int_{0}^{\frac{\pi }{2}}sin^2xdx\) và \(\int_{0}^{\frac{\pi }{2}}cos^2x dx\). Hãy chỉ ra khẳng định đúng:
(A) \(\int_{0}^{\frac{\pi }{2}}sin^2xdx >\int_{0}^{\frac{\pi }{2}}cos^2x dx\)
(B) \(\int_{0}^{\frac{\pi }{2}}sin^2xdx <\int_{0}^{\frac{\pi }{2}}cos^2x dx\)
(C) \(\int_{0}^{\frac{\pi }{2}}sin^2xdx =\int_{0}^{\frac{\pi }{2}}cos^2x dx\)(D) Không so sánh được
-
Bài tập 5 trang 128 SGK Giải tích 12
Diện tích hình phẳng giới hạn bởi các đường cong:
Câu a: \(y=x^3\) và \(y=x^5\) bằng:
(A). 0
(B). -4
(C). \(\frac{1}{6}\)
(D). 2
Câu b: \(y=x+sinx\)
(A). -4
(B). 4
(C). 0
(D). 1
-
Bài tập 6 trang 128 SGK Giải tích 12
Cho hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\) và \(y=x\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
(A). 0
(B). \(-\pi\)
(C). \(\pi\)
(D). \(\frac{\pi}{6}\)
-
Bài tập 41 trang 175 SGK Toán 12 NC
Tìm nguyên hàm của các hàm số sau:
\(\begin{array}{*{20}{l}}
{a)y = 2x(1 - x - 3)}\\
{b)y = 8x - \frac{2}{{{x^{\frac{1}{4}}}}}}\\
{c)y = {x^{\frac{1}{2}}}\sin \left( {{x^{\frac{3}{2}}} + 1} \right)}\\
{d)y = \frac{{\sin (2x + 1)}}{{{{\cos }^2}(2x + 1)}}}
\end{array}\) -
Bài tập 42 trang 175 SGK Toán 12 NC
Tìm nguyên hàm của các hàm số sau:
\(\begin{array}{l}
a)y = \frac{1}{{{x^2}}}\cos \left( {\frac{1}{x} - 1} \right)\\
b)y = {x^3}{\left( {1 + {x^4}} \right)^3}\\
c)y = \frac{{x{e^{2x}}}}{3}\\
d)y = {x^2}{e^x}
\end{array}\) -
Bài tập 43 trang 176 SGK Toán 12 NC
Tìm nguyên hàm của các hàm số sau:
a. y = x.e-x
b. \(y = \frac{{\ln x}}{x}\)
-
Bài tập 44 trang 176 SGK Toán 12 NC
Tìm hàm số y = f(x) nếu biết dy = 12x(3x2 − 1)3dx và f(1) = 3
-
Bài tập 45 trang 176 SGK Toán 12 NC
Xác định số b dương để tích phân \(\int\limits_0^b {(x - {x^2})dx} \) có giá trị lớn nhất.
-
Bài tập 46 trang 176 SGK Toán 12 NC
Cho biết \(\int\limits_7^9 {f(x)dx} = - 1,\)
\(\int\limits_7^9 {f(x)dx} = 5,\int\limits_7^9 {g(x)dx} = 4.\)
Hãy tìm:
\(\begin{array}{l}
a)\int \limits_1^9 - 2f\left( x \right)dx\\
b)\int \limits_7^9 \left[ {f\left( x \right) + g\left( x \right)} \right]dx\\
c)\int\limits_7^9 {[2f(x) - 3g(x)]dx} \\
d)\int\limits_1^7 {f(x)dx}
\end{array}\) -
Bài tập 47 trang 176 SGK Toán 12 NC
Cho hàm số f liên tục trên [a; b]. Tỉ số: \(\frac{1}{{b - a}} - \int_a^b {f(x)dx} \) được gọi là giá trị trung bình của hàm số f trên [a;b] và được kí hiệu là m(f). Chứng minh rằng tồn tại điểm c ∈ [a; b] sao cho m(f) = f(c)
-
Bài tập 48 trang 176 SGK Toán 12 NC
Giả sử một vật từ trạng thái nghỉ khi t = 0 (s) chuyển động thẳng với vận tốc v(t) = t(5 − t) (m/s). Tìm quãng đường vật đi được cho tới khi nó dừng lại.
-
Bài tập 49 trang 176 SGK Toán 12 NC
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. biết rằng B đuổi kịp A sau 8 giây ( kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
-
Bài tập 50 trang 176 SGK Toán 12 NC
Tính các tích phân sau:
\(\begin{array}{l}
a)\int_0^{\frac{\pi }{2}} {{x^2}sin2xdx} \\
b)\int_1^2 {x(2{x^2} + 1)dx} \\
c)\int_2^3 {(x - 1){e^{{x^2} - 2x}}dx}
\end{array}\) -
Bài tập 51 trang 176 SGK Toán 12 NC
Tính diện tích các hình phẳng giới hạn bởi:
a) Đồ thị các hàm số y = 4 − x2; y = -x + 2
b) Các đường cong có phương trình x = 4 − 4y2 và x = 1 − y4 trong miền x ≥ 0.
-
Bài tập 52 trang 177 SGK Toán 12 NC
Tính diện tích của các hình phẳng giới hạn bởi:
a) Parabol y = x2 − 2x + 2, tiếp tuyến của nó tại điểm M(3; 5) và trục tung
b) Parabol y = −x2 + 4x − 3y và các tiếp tuyến của nó tại các điểm A(0;−3) và B(3;0)
-
Bài tập 53 trang 177 SGK Toán 12 NC
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 2, biết rằng thiết diện của vật thể bị cắt bơi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ (0 ≤ x ≤ 2) là một nửa hình tròn đường kính \(\sqrt 5 {x^2}\)
-
Bài tập 54 trang 177 SGK Toán 12 NC
Xét hình phẳng giới hạn bởi đường hypebol y = 2/x và các đường thẳng y = 1, y = 4, x = 0. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng đó quanh trục tung.
-
Bài tập 55 trang 177 SGK Toán 12 NC
Cho hình phẳng A được giới hạn bởi đồ thị hàm số: \(y = \sqrt {\cos x} \left( {0 \le x \le \frac{\pi }{2}} \right)\) và hai trục tọa độ. Tính thể tích khối tròn xoay tọa thành khi quay hình đó quay trục tung.
-
Bài tập 56 trang 177 SGK Toán 12 NC
Cho hình phẳng A được giới hạn bởi đường cong có phương trình x(y + 1) = 2 và các đường thẳng x = 0, y = 0, y = 3. Tính thể tích khối tròn xoay tạo được khi quay A quanh trục tung.
-
Bài tập 57 trang 177 SGK Toán 12 NC
Cho hình phẳng A được giới hạn bởi đường cong có phương trình x − y2 = 0 và các đường thẳng y = 2, x = 0. Tính thể tích khối tròn xoay tạo thành khi quay A.
a) Quanh trục hoành;
b) quanh trục tung
-
Bài tập 58 trang 177 SGK Toán 12 NC
Cho hình phẳng A được giới hạn bởi đường cong có phương trình \(y = {x^{\frac{1}{2}}}{e^{\frac{x}{2}}}\) và các đường thẳng x = , x = 2, y = 0.Tính thể tích khối tròn xoay tạo thành khi quay A quanh trục hoành.
-
Bài tập 59 trang 177 SGK Toán 12 NC
Cho hình phẳng A được giới hạn bởi đường cong có phương trình y2 = x3 và các đường thẳng y = 0, x = 1. Tính thể tích khối tròn xoay tạo được khi quay A
a) Quanh trục hoành
b) Quanh trục tung.
-
Bài tập 60 trang 178 SGK Toán 12 NC
Giả sử \(\int\limits_1^5 {\frac{{dx}}{{2x - 1}}} = \ln c\). Giá trị của c là
(A) 9(B) 3
(C) 81
(D) 8
-
Bài tập 61 trang 178 SGK Toán 12 NC
Giá trị của \(\int\limits_0^2 {2{e^{2x}}dx} \) là
\(\left( A \right)\,{e^4}\); \(\left( B \right)\,{e^4} - 1;\)
\(\left( C \right)\,4{e^4};\) \(\left( D \right)\,3{e^4} - 1;\)
-
Bài tập 62 trang 178 SGK Toán 12 NC
Giá trị của \(\int \limits_{ - 1}^0 {x^2}{\left( {x + 1} \right)^3}dx\) là:
(A) \( - \frac{7}{{10}}\)
(B) \( - \frac{6}{{10}}\)
(C) \(\frac{2}{{15}}\)
(D) \(\frac{1}{{60}}\)
-
Bài tập 63 trang 178 SGK Toán 12 NC
Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bởi đường thẳng y = 4x và đồ thị hàm số y = x3 là:
(A) 4
(B) 5
(C) 3
(D) 3,5
-
Bài tập 64 trang 178 SGK Toán 12 NC
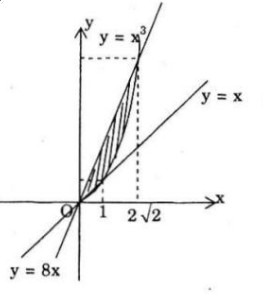
Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bới hai đường thẳng \(y = 8x,y = x\) và đồ thị hàm số \(y = {x^3}\) là:
(A) 12
(B) 15,75
(C) 6,75
(D) 4
-
Bài tập 65 trang 178 SGK Toán 12 NC
Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bởi đường thẳng y = 2x và đồ thị hàm số y = x2 là:
(A) \(\frac{4}{3}\)
(B) \(\frac{3}{2}\)
(C) \(\frac{5}{3}\)
(D) \(\frac{{23}}{{15}}\)
-
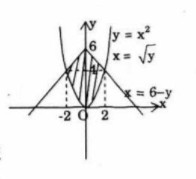
Bài tập 66 trang 179 SGK Toán 12 NC
Cho hình phẳng A được giới hạn bởi đồ thị hàm hai số \(y = {x^2}\) và \(y = 6 - \left| x \right|\). Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung:
(A) \(\frac{{32\pi }}{3}\)
(B) \(9\pi \)
(C) \(8\pi \)
(D) \(\frac{{20\pi }}{3}\)
-
Bài tập 67 trang 179 SGK Toán 12 NC
Cho a, b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai được giới hạn bởi parabol y = ax2 và đường thẳng y = −bx. Biết rằng thể tích khối tròn xoay tạo được khi quay K xung quanh trục hoành là một số không phụ thuộc vào giá trị của a và b. Khi đó a và b thỏa mãn điều kiện sau:
(A) \({b^4} = 2{a^5}\)
(B) \({b^3} = 2{a^5}\)
(C) \({b^5} = 2{a^3}\)
(D) \({b^4} = 2{a^2}\)
-
Bài tập 3.43 trang 180 SBT Toán 12
Tính các nguyên hàm sau:
a) \(\int (2x - 3)\sqrt {x - 3} dx\), đặt \(u = \sqrt {x - 3} \)
b) \(\int \frac{x}{{{{(1 + {x^2})}^{\frac{3}{2}}}}}dx\), đặt \(u = \sqrt {{x^2} + 1} \)
c) \(\int \frac{{{e^x}}}{{{e^x} + {e^{ - x}}}}dx\), đặt \(u = {e^{2x}} + 1\)
d) \(\int \frac{1}{{\sin x - \sin a}}dx\)
-
Bài tập 3.44 trang 180 SBT Toán 12
Tính các tích phân sau:
a) \(\int \limits_0^1 {(y - 1)^2}\sqrt y dy\), đặt \(t = \sqrt y \)
b) \(\int \limits_1^2 ({z^2} + 1)\sqrt[3]{{{{(z - 1)}^2}}}dz\), đặt \(u = \sqrt[3]{{{{(z - 1)}^2}}}\)
c) \(\int \limits_1^e \frac{{\sqrt {4 + 5\ln x} }}{x}dx\)
d) \(\int \limits_0^{\frac{\pi }{2}} ({\cos ^5}\varphi - {\sin ^5}\varphi )d\varphi \)
-
Bài tập 3.45 trang 181 SBT Toán 12
Tính các tích phân sau:
a) \(\int \limits_0^{\frac{\pi }{4}} \cos 2x.{\cos ^2}xdx\)
b) \(\int \limits_{\frac{1}{2}}^1 \frac{{{e^x}}}{{{e^{2x}} - 1}}dx\)
c) \(\int \limits_0^1 \frac{{x + 2}}{{{x^2} + 2x + 1}}\ln (x + 1)dx\)
d) \(\int \limits_0^{\frac{\pi }{4}} \frac{{x\sin x + (x + 1)\cos x}}{{x\sin x + \cos x}}dx\)
-
Bài tập 3.46 trang 181 SBT Toán 12
Tính diện tích các hình phẳng giới hạn bởi các đường sau:
a) \(y = x - 1 + \frac{{\ln x}}{x},y = x - 1\) và x = e;
b) \(y = {x^3} - {x^2}\) và \(y = \frac{1}{9}(x - 1)\);
-
Bài tập 3.47 trang 181 SBT Toán 12
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi
a) \(y = {x^{\frac{2}{3}}},x = 0\) và tiếp tuyến với đường \(y = {x^{\frac{2}{3}}}\) tại điểm có hoành độ x = 1, quanh trục Oy;
b) \(y = \frac{1}{x} - 1,y = 0,y = 2x\), quanh trục Ox.
c) \(y = \left| {2x - {x^2}} \right|,y = 0\) và x = 3, quanh :
* Trục Ox
* Trục Oy
-
Bài tập 3.48 trang 181 SBT Toán 12
Hãy chỉ ra các kết quả đúng trong các kết quả sau:
a) \(\int \limits_0^1 {x^n}{(1 - x)^m}dx = \int \limits_0^1 {x^m}{(1 - x)^n}dx;m,n \in {N^ * }\)
b) \(\int \limits_{ - 1}^1 \frac{{{t^2}}}{{{e^t} + 1}}dt = \int \limits_0^1 {t^2}dt\)
c) \(\int \limits_0^1 {\sin ^3}x\cos xdx = \int \limits_0^1 {t^3}dt\)
-
Bài tập 3.49 trang 182 SBT Toán 12
Hàm số nào dưới đây không là nguyên hàm của hàm số \(f\left( x \right) = \frac{{x\left( {2 + x} \right)}}{{{{\left( {x + 1} \right)}^2}}}\)?
A. \(\frac{{{x^2} + x - 1}}{{x + 1}}\)
B. \(\frac{{{x^2} - x - 1}}{{x + 1}}\)
C. \(\frac{{{x^2} + x + 1}}{{x + 1}}\)
D. \(\frac{{{x^2}}}{{x + 1}}\)
-
Bài tập 3.50 trang 182 SBT Toán 12
Nếu \(\int \limits_a^d f\left( x \right)dx = 5,\int \limits_b^d f\left( x \right)dx = 2\)
với a < d < b thì \(\int \limits_a^b f\left( x \right)dx\) bằng
A. - 2
B. 8
C. 0
D. 3
-
Bài tập 3.51 trang 182 SBT Toán 12
Tìm khẳng định sai trong các khẳng định sau:
A. \(\int \limits_0^1 \sin \left( {1 - x} \right)dx = \mathop \smallint \limits_0^1 \sin xdx\)
B. \(\int \limits_0^\pi \sin \frac{x}{2}dx = 2\mathop \smallint \limits_0^{\frac{\pi }{2}} \sin xdx\)
C. \(\int \limits_0^1 {\left( {1 + x} \right)^x}dx = 0\)
D. \(\int \limits_{ - 1}^1 {x^{2007}}\left( {1 + x} \right)dx = \frac{2}{{2009}}\)
-
Bài tập 3.52 trang 182 SBT Toán 12
Tìm khẳng định đúng trong các khẳng định sau:
A. \(\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = \int \limits_0^\pi \left| {\sin \left( {x - \frac{\pi }{4}} \right)} \right|dx\)
B. \(\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = \int \limits_0^\pi \left| {\cos \left( {x + \frac{\pi }{4}} \right)} \right|dx\)
C. \(\begin{array}{l}
\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx\\
= \int \limits_0^{\frac{{3\pi }}{4}} \sin \left( {x + \frac{\pi }{4}} \right)dx - \int \limits_{\frac{{3\pi }}{4}}^\pi \sin \left( {x + \frac{\pi }{4}} \right)dx
\end{array}\)D. \(\int \limits_0^\pi \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = 2\int \limits_0^{\frac{\pi }{4}} \sin \left( {x + \frac{\pi }{4}} \right)dx\)
-
Bài tập 3.53 trang 183 SBT Toán 12
\(\int \limits_0^1 x{e^{1 - x}}dx\) bằng
A. 1 - e
B. e - 2
C. 1
D. - 1
-
Bài tập 3.54 trang 183 SBT Toán 12
Nhờ ý nghĩa hình học của tích phân, hãy tìm khẳng định sai trong các khẳng định sau:
A. \(\displaystyle \int\limits_0^1 {\ln \left( {1 + x} \right)dx} > \int\limits_0^1 {\frac{{x - 1}}{{e - 1}}dx} \)
B. \(\displaystyle \int\limits_0^{\frac{\pi }{4}} {{{\sin }^2}xdx} < \int\limits_0^{\frac{\pi }{4}} {\sin 2xdx} \)
C. \(\displaystyle \int\limits_0^1 {{e^{ - x}}dx} > \int\limits_0^1 {{{\left( {\frac{{1 - x}}{{1 + x}}} \right)}^2}dx} \)
D. \(\displaystyle \int\limits_0^1 {{e^{ - {x^2}}}dx} > \int\limits_0^1 {{e^{ - {x^3}}}dx} \)
-
Bài tập 3.55 trang 183 SBT Toán 12
Thể tích của khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các đường \(y = {\left( {1 - x} \right)^2},y = 0\), x = 0 và x = 2 bằng
A. \(\frac{{8\pi \sqrt 2 }}{3}\)
B. \(\frac{{2\pi }}{5}\)
C. \(\frac{{5\pi }}{2}\)
D. \(2\pi \)
-
Bài tập 3.56 trang 183 SBT Toán 12
\(\int \limits_{ - \frac{1}{2}}^{\frac{1}{2}} \frac{{x\left( {1 + {x^2} + {x^4}} \right)}}{{1 + {x^2}}}dx\) bằng
A. 0
B. 1
C. - 1
D. 2
-
Bài tập 3.67 trang 183 SBT Toán 12
Khẳng định nào sau đây sai?
A. \(\int \limits_{\frac{\pi }{2}}^\pi \frac{{\sin x}}{x}dx < \int \limits_{\frac{\pi }{2}}^\pi \frac{{\cos x}}{x}dx\)
B. \(\int \limits_{\frac{\pi }{4}}^1 \frac{{\tan x}}{x}dx > \int \limits_{\frac{\pi }{4}}^1 \frac{{\cot x}}{x}dx\)
C. \(\int \limits_0^{\frac{\pi }{4}} {\sin ^4}xdx < \int \limits_0^{\frac{\pi }{2}} dx\)
D. \(\int \limits_1^e \frac{{\ln x}}{x}dx < \int \limits_1^e \frac{{{e^x}}}{x}dx\)
-
Bài tập 3.58 trang 184 SBT Toán 12
Diện tích của hình phẳng được giới hạn bởi các đường \(\displaystyle y = \tan x,y = 0,x = - \frac{\pi }{4}\) và \(\displaystyle x = \frac{\pi }{4}\) bằng
A. \(\displaystyle \pi \) B. \(\displaystyle - \pi \)
C. \(\displaystyle \ln 2\) D. \(\displaystyle 0\)
-
Bài tập 3.59 trang 184 SBT Toán 12
Thể tích khối tròn xoay tạo bởi phép quay quanh trục \(\displaystyle Ox\) của hình phẳng giới hạn bởi các đường \(\displaystyle y = {\sin ^{\frac{3}{2}}}x,y = 0,x = 0\) và \(\displaystyle x = \frac{\pi }{2}\) bằng
A. \(\displaystyle 1\) B. \(\displaystyle \frac{2}{7}\)
C. \(\displaystyle 2\pi \) D. \(\displaystyle \frac{2}{3}\pi \)
-
Bài tập 3.60 trang 184 SBT Toán 12
Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) = - 5t + 10\left( {m/s} \right)\), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển bao nhiêu mét?
A. 0,2m
B. 2m
C. 10m
D. 20m






