Giải bài 5 tr 134 sách GK Toán GT lớp 12
Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện:
a) |z| = 1.
b) |z| ≤ 1.
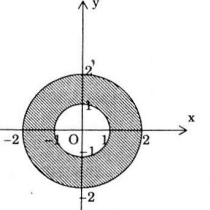
c) 1 < |z| ≤ 2.
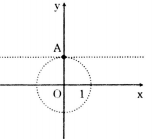
d) |z| = 1 và phần ảo của z bằng 1.
Hướng dẫn giải chi tiết bài 5
Phương pháp:
Đặt \(z=x+yi (x,y\in\mathbb{R})\) khi đó trên mặt phẳng toạ độ Oxy, điểm M(x;y) biểu diễn số phức z.
Dựa vào dữ kiện đề bài ta xác định tập hợp các điểm biểu diễn số phức z.
Lời giải:
Ta có lời giải chi tiết câu a, b, c, d bài 4 như sau:
Câu a:
Đặt \(z=x+yi (x,y\in\mathbb{R})\)
Ta có |z| = 1 ⇔  = 1 ⇔ x2 + y2 = 1.
= 1 ⇔ x2 + y2 = 1.
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tam O, bán kính bằng 1.
.PNG)
Câu b:
Ta có |z| ≤ 1 ⇔  ≤ 1 ⇔ x2 + y2 ≤ 1.
≤ 1 ⇔ x2 + y2 ≤ 1.
Vậy tập hợp điểm biểu diễn số phức z là hình tròn tâm O, bán kính bằng 1 (kể cả các điểm trên đường tròn x2+y2=1).
Câu c:
Ta có 1<|z| ≤ 2 ⇔ 1 <  ≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
Vậy tập hợp điểm biểu diễn số phức z là phần nằm giữa đường tròn tâm O, bán kính bằng 1 (không kể điểm trên đường tròn này) và đường tròn tâm O, bán kính bằng 2 (kể cả các điểm trên đường tròn này).
Câu d:
Ta có |z| = 1 ⇔  = 1 ⇔ x2 + y2 = 1 và phần ảo của z bằng 1 tức y = 1.
= 1 ⇔ x2 + y2 = 1 và phần ảo của z bằng 1 tức y = 1.
Suy ra x = 0 và y = 1.
Vậy tập hợp các điểm cần tìm là điểm A(0;1).
-- Mod Toán 12 HỌC247
-


Viết số phức sau dưới dạng lượng giác: \(\eqalign{2i\left( {\sqrt 3 - i} \right)} \)
bởi truc lam
 07/05/2021
07/05/2021
Viết số phức sau dưới dạng lượng giác: \(\eqalign{2i\left( {\sqrt 3 - i} \right)} \)
Theo dõi (0) 1 Trả lời -


Viết số phức sau dưới dạng lượng giác: \(\eqalign{1 - i\sqrt 3 ;1 + i;(1 - i\sqrt 3 )(1 + i);{{1 - i\sqrt 3 } \over {1 + i}}}\)
bởi minh thuận
 07/05/2021
07/05/2021
Viết số phức sau dưới dạng lượng giác: \(\eqalign{1 - i\sqrt 3 ;1 + i;(1 - i\sqrt 3 )(1 + i);{{1 - i\sqrt 3 } \over {1 + i}}}\)
Theo dõi (0) 1 Trả lời -


Hãy tìm dạng lượng giác của các số phức: \(\overline z \,;\, - z;\,{1 \over {\overline z }};\,kz\,\left( {k \in \mathbb R^*} \right)\) trong trường hợp sau: \(z = 1 + \sqrt 3 i.\)
bởi Hồng Hạnh
 07/05/2021
07/05/2021
Hãy tìm dạng lượng giác của các số phức: \(\overline z \,;\, - z;\,{1 \over {\overline z }};\,kz\,\left( {k \in \mathbb R^*} \right)\) trong trường hợp sau: \(z = 1 + \sqrt 3 i.\)
Theo dõi (0) 1 Trả lời -


Hãy tìm dạng lượng giác của các số phức: \(\overline z \,;\, - z;\,{1 \over {\overline z }};\,kz\,\left( {k \in \mathbb R^*} \right)\) trong trường hợp sau: \(z = r\left( {\cos \varphi + i\sin\varphi } \right)\,\left( {r > 0} \right);\)
bởi Kim Xuyen
 06/05/2021
06/05/2021
Hãy tìm dạng lượng giác của các số phức: \(\overline z \,;\, - z;\,{1 \over {\overline z }};\,kz\,\left( {k \in \mathbb R^*} \right)\) trong trường hợp sau: \(z = r\left( {\cos \varphi + i\sin\varphi } \right)\,\left( {r > 0} \right);\)
Theo dõi (0) 1 Trả lời -


Tìm các số thực a, b, c để phương trình (với ẩn z): \({z^3} + a{z^2} + bz + c = 0\) nhận \(z = 1 + i\) làm nghiệm và cũng nhận \(z = 2\) là nghiệm.
bởi Thanh Thanh
 07/05/2021
07/05/2021
Tìm các số thực a, b, c để phương trình (với ẩn z): \({z^3} + a{z^2} + bz + c = 0\) nhận \(z = 1 + i\) làm nghiệm và cũng nhận \(z = 2\) là nghiệm.
Theo dõi (0) 1 Trả lời -


Hãy tìm các số thực b, c để phương trình (với ẩn z): \({z^2} + bz + c = 0\) nhận \(z = 1 + i\) làm một nghiệm.
bởi Sasu ka
 07/05/2021
07/05/2021
Hãy tìm các số thực b, c để phương trình (với ẩn z): \({z^2} + bz + c = 0\) nhận \(z = 1 + i\) làm một nghiệm.
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(8{z^4} + 8{z^3} = z + 1\).
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \({z^4} + 4 = 0\).
bởi Lê Minh Bảo Bảo
 07/05/2021
07/05/2021
Giải phương trình sau: \({z^4} + 4 = 0\).
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \({z^4} - 1 = 0\);
bởi A La
 07/05/2021
07/05/2021
Giải phương trình sau: \({z^4} - 1 = 0\);
Theo dõi (0) 1 Trả lời -


Giải phương trình sau trên C: \({z^3} + 1 = 0\);
bởi Truc Ly
 07/05/2021
07/05/2021
Giải phương trình sau trên C: \({z^3} + 1 = 0\);
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3 trang 134 SGK Giải tích 12
Bài tập 4 trang 134 SGK Giải tích 12
Bài tập 6 trang 134 SGK Giải tích 12
Bài tập 4.1 trang 198 SBT Toán 12
Bài tập 4.2 trang 198 SBT Toán 12
Bài tập 4.3 trang 199 SBT Toán 12
Bài tập 4.4 trang 199 SBT Toán 12
Bài tập 4.5 trang 199 SBT Toán 12
Bài tập 4.6 trang 199 SBT Toán 12
Bài tập 4.7 trang 200 SBT Toán 12
Bài tập 1 trang 189 SGK Toán 12 NC
Bài tập 2 trang 189 SGK Toán 12 NC
Bài tập 3 trang 189 SGK Toán 12 NC
Bài tập 4 trang 189 SGK Toán 12 NC
Bài tập 5 trang 190 SGK Toán 12 NC
Bài tập 6 trang 190 SGK Toán 12 NC
Bài tập 7 trang 190 SGK Toán 12 NC
Bài tập 8 trang 190 SGK Toán 12 NC
Bài tập 9 trang 190 SGK Toán 12 NC
Bài tập 10 trang 190 SGK Toán 12 NC
Bài tập 11 trang 191 SGK Toán 12 NC
Bài tập 12 trang 191 SGK Toán 12 NC
Bài tập 13 trang 191 SGK Toán 12 NC
Bài tập 14 trang 191 SGK Toán 12 NC




.PNG)