B├Āi tß║Łp trß║»c nghiß╗ćm To├Īn 12 B├Āi 1 vß╗ü Sß╗æ phß╗®c online ─æß║¦y ─æß╗¦ ─æ├Īp ├Īn v├Ā lß╗Øi giß║Żi gi├║p c├Īc em tß╗▒ luyß╗ćn tß║Łp v├Ā cß╗¦ng cß╗æ kiß║┐n thß╗®c b├Āi hß╗Źc.
C├óu hß╗Åi trß║»c nghiß╗ćm (10 c├óu):
-
Câu 1:
Cho sß╗æ phß╗®c \(z = ax + bi\,\left( {a,b \in R} \right)\), mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy l├Ā sai?
- A. ─Éß╗æi vß╗øi sß╗æ phß╗®c z, a l├Ā phß║¦n thß╗▒c.
- B. ─Éiß╗ām \(M\left( {a,b} \right)\) trong mß╗Öt hß╗ć tß╗Źa ─æß╗Ö vu├┤ng g├│c cß╗¦a mß║Ęt phß║│ng phß╗®c ─æŲ░ß╗Żc gß╗Źi l├Ā ─æiß╗ām biß╗āu diß╗ģn sß╗æ phß╗®c \(z = a + bi\).
- C. ─Éß╗æi vß╗øi sß╗æ phß╗®c z, bi l├Ā phß║¦n ß║Żo.
- D. Sß╗æ i ─æŲ░ß╗Żc gß╗Źi l├Ā ─æŲĪn vß╗ŗ ß║Żo.
-
- A. \(M\left( {5; - 3} \right)\)
- B. \(N\left( { - 3;5} \right)\)
- C. \(P\left( { - 5;3} \right)\)
- D. \(Q\left( {3; - 5} \right)\)
-
- A. Sß╗æ phß╗®c \(z=a+bi\) ─æŲ░ß╗Żc biß╗āu diß╗ģn bß║▒ng ─æiß╗ām M(a;b) trong mß║Ęt phß║│ng phß╗®c Oxy
- B. Sß╗æ phß╗®c \(z=a+bi\)ŌĆŗ c├│ m├┤─æun l├Ā \(\sqrt {{a^2} + {b^2}}\)
- C. Sß╗æ phß╗®c \(z=a+bi\) th├¼ a=0 v├Ā b=0
- D. Sß╗æ phß╗®c \(z=a+bi\) c├│ sß╗æ phß╗®c li├¬n hß╗Żp l├Ā \(\overline z = - a - bi\)
-
- A. ─ÉŲ░ß╗Øng tr├▓n \({x^2} + {y^2} = 4\)
- B. ─ÉŲ░ß╗Øng thß║│ng y=2
- C. ─ÉŲ░ß╗Øng thß║│ng x=2
- D. Hai ─æŲ░ß╗Øng thß║│ng x=2 v├Ā y=2
-
Câu 5:
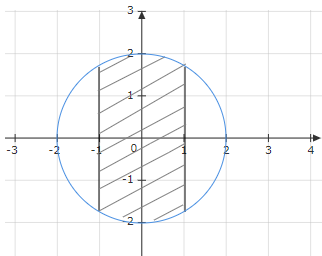
Sß╗æ phß╗®c thß╗Åa m├Żn ─æiß╗üu kiß╗ćn n├Āo th├¼ c├│ ─æiß╗ām biß╗āu diß╗ģn ß╗¤ phß║¦n gß║Īch ch├®o?
- A. Sß╗æ phß╗®c c├│ phß║¦n thß╗▒c nß║▒m trong \(\left( { - 1;1} \right)\) v├Ā m├┤ ─æun nhß╗Å hŲĪn 2
- B. Sß╗æ phß╗®c c├│ phß║¦n thß╗▒c nß║▒m trong \(\left[ { - 1;1} \right]\) v├Ā m├┤ ─æun nhß╗Å hŲĪn 2
- C. Sß╗æ phß╗®c c├│ phß║¦n thß╗▒c nß║▒m trong \(\left[ { - 1;1} \right]\) v├Ā m├┤ ─æun kh├┤ng vŲ░ß╗Żt qu├Ī 2
- D. Sß╗æ phß╗®c c├│ phß║¦n thß╗▒c nß║▒m trong \(\left( { - 1;1} \right)\) v├Ā m├┤ ─æun kh├┤ng vŲ░ß╗Żt qu├Ī 2
-
- A. \(a^2+b^2\)
- B. \(a^2-b^2\)
- C. a+b
- D. a-b
-
- A. Ph├ó╠Ćn thŲ░╠Żc cu╠ēa z la╠Ć 2.
- B. Ph├ó╠Ćn a╠ēo cu╠ēa z la╠Ć -2.
- C. S├┤╠ü phŲ░╠üc li├¬n hŲĪ╠Żp cu╠ēa z la╠Ć \(\overline z = - 2 + 2i\)
- D. \(\left| z \right| = \sqrt {{2^2} + {{\left( { - 2} \right)}^2}} = 2\sqrt 2 \)
-
- A. x = 3, y = 1
- B. x = 3, y = -1
- C. x = -3, y = -1
- D. x = -3, y = 1
-
- A. x = 2, y = -2
- B. x = -2, y = -2
- C. x = 2, y = 2
- D. x = -2, y = 2
-
- A. Hai ─æiß╗ām
- B. Hai ─æŲ░ß╗Øng thß║│ng
- C. ─ÉŲ░ŲĪ╠Ćng tro╠Ćn ba╠ün ki╠ünh R = 2
- D. ─ÉŲ░ŲĪ╠Ćng tro╠Ćn ba╠ün ki╠ünh R = \(\sqrt 2 \)