Bài tập 90 trang 104 SGK Toán 9 Tập 2

Hướng dẫn giải

+) Đường tròn ngoại tiếp hình vuông là đường tròn đi qua tất cả các đỉnh của hình vuông.

+) Đường tròn nội tiếp hình vuông là đường tròn tiếp xúc với tất cả các cạnh của hình vuông.

+) Sử dụng định lý Pytago để tính toán.

Lời giải chi tiết

a) Dùng êke ta vẽ hình vuông \(ABCD\) có cạnh bằng \(4cm\) như sau:

- Vẽ \(AB = 4cm\).

- Vẽ \(BC \bot AB\) và \(BC = 4cm\)

- Vẽ \(DC\bot BC\) và \(DC = 4cm\)

- Nối \(D\) với \(A\), ta có \(AD\bot DC\) và \(AD = 4cm\)

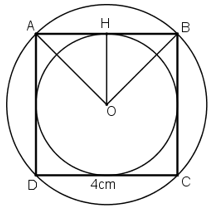
b) Ta có ABCD là hình vuông. Gọi O là giao điểm của 2 đường chéo AC và BD khi đó ta có: \(OA = OB = OC = OD.\) Nên \(O\) chính là tâm của đường tròn ngoại tiếp hình vuông.

Tam giác \(ABC\) là tam giác vuông cân nên \(AB = BC\).

Áp dụng định lí Pytago trong tam giác vuông \(ABC\), ta có: 

\(\eqalign{
& A{C^2} = A{B^2} + B{C^2} = 2{\rm{A}}{B^2} \Leftrightarrow A{C^2} = {2.4^2} = 32 \cr
& \Rightarrow AC = \sqrt {32} = 4\sqrt 2 \cr}\)

Vậy \(\displaystyle AO = R = {{AC} \over 2} = {{4\sqrt 2 } \over 2} = 2\sqrt 2 \) 

Vậy \(R  = 2\sqrt{2}\) \(cm\)

c) Vẽ \(OH \bot DC\).Tương tự ta kẻ từ O các đường vuông góc đến các cạnh AD, AB, BC. Khi đó ta có

Đường tròn tâm \(O\), bán kính \(OH\). Đó là đường tròn nội tiếp hình vuông \(ABCD\)

Ta có: \(\displaystyle OH = {{A{\rm{D}}} \over 2} = 2(cm)\)  

Vậy \(r = OH = 2cm\)

-- Mod Toán 9 HỌC247