Bài tập 3.1 trang 114 SBT Toán 9 Tập 2

31 BT SGK

Bài tập 3.1 tr 114 sách BT Toán lớp 9 Tập 2

Cho tam giác đều $ACB$ và $ACD,$ cạnh $a.$ Lần lượt lấy $B$ và $D$ làm tâm vẽ hai đường tròn bán kính $a.$ Kẻ các đường kính $ABE$ và $ADF.$ Trên cung nhỏ $CE$ của đường tròn tâm $B$ lấy điểm $M$ (không trùng với $E$ và $C$). Đường thẳng $CM$ cắt đường tròn tâm $D$ tại điểm thứ hai là $N.$ Hai đường thẳng $EM$ và $NF$ cắt nhau tại điểm $T.$ Gọi $H$ là giao điểm của $AT$ và $MN.$ Chứng minh:

$a)$ $MNT$ là tam giác đều.

$b)$ $AT = 4AH.$

Hình học 9 Chương 3 Bài 11 Trắc nghiệm Hình học 9 Chương 3 Bài 11 Giải bài tập Hình học 9 Chương 3 Bài 11

Hướng dẫn giải chi tiết

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.

+) Góc nội tiếp chắn nửa đường tròn là góc vuông.

+) Sử dụng tính chất đường trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Lời giải chi tiết

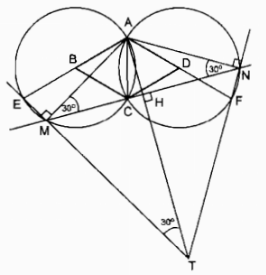
a) Trong đường tròn (B) ta có:

$\widehat {AMC} = {1 \over 2}\widehat {ABC}$ (hệ quả góc nội tiếp) mà $\widehat {ABC} = 60^\circ $ (vì ∆ABC đều)

$ \Rightarrow \widehat {AMC} = 30^\circ $

$\widehat {AME} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn (B))

$ \Rightarrow \widehat {AMT} = 90^\circ $

$\widehat {TMN} = \widehat {AMT} - \widehat {AMC} = 90^\circ - 30^\circ = 60^\circ $

Trong đường tròn (D) ta có:

$\widehat {ANC} = {1 \over 2}\widehat {ADC}$ (Hệ quả góc nội tiếp) mà $\widehat {ADC} = 60^\circ $ (vì ∆ADC đều) $ \Rightarrow \widehat {ANC} = 30^\circ $

$\widehat {ANF} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn (D))

$ \Rightarrow \widehat {ANC} + \widehat {CNF} = 90^\circ \Rightarrow \widehat {CNF} = 90^\circ - \widehat {ANC} = 90^\circ - 30^\circ = 60^\circ $ hay $\widehat {MNT} = 60^\circ $

Vậy ∆TMN đều.

b) $\widehat {AMC} = \widehat {ANC} = 30^\circ $

$ \Rightarrow \Delta AMN$ cân tại A $ \Rightarrow $ AM = AN nên A nằm trên đường trung trực MN ∆TMN đều

$ \Rightarrow $ TM = TN nên T nằm trên đường trung trực MN

Suy ra AT là đường trung trực của MN nên AT ⊥ MN

∆AHM có $\widehat {AHM} = 90^\circ $

$AM = {{AH} \over {\sin M}} = {{AH} \over {\sin 30^\circ }} = {{AH} \over {{1 \over 2}}} = 2AH$ (1)

TH ⊥ MN nên TH là đường phân giác của $\widehat T$ nên $\widehat {MTA} = 30^\circ $

∆AMT có $\widehat {AMT} = 90^\circ $

$AT = {{AT} \over {\sin \widehat {MTA}}} = {{AM} \over {{1 \over 2}}} = 2AM$ (2)

Từ (1) và (2) suy ra: AT = 4AH

-- Mod Toán 9 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 3.1 trang 114 SBT Toán 9 Tập 2 HAY thì click chia sẻ

YOMEDIA

Chứng minh rằng đường trung trực của đoạn HD đi qua điểm I

bởi Choco Choco 25/01/2019

Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O), các đường cao AD và CE cắt nhau tại H. Đường tròn (I) ngoại tiếp tam giác BDH cắt đường tròn (O) tại M (M khác B). Vẽ đường kính BF của đường tròn (O).

a) Chứng minh rằng: Đường trung trực của đoạn HD đi qua điểm I.

b) Gọi N là giao điểm của HF và AC. Chứng minh NE là tiếp tuyến của đường tròn (I).

c) Chứng minh ba điểm M, H, F thẳng hàng.

Theo dõi (0) 1 Trả lời
Chứng minh △BOO' đồng dạng △BCD

bởi Lê Minh Trí 25/01/2019

Chỉ vì th trực nhật lớp xóa mất hình cô vẽ mất 15 phút nên bị cô phạt cả lớp làm bài nàyT-T:

Cho (O) Vvà (O') cắt nhau tại 2 điểm A,B (O và O' thộc 2 nửa mặt phẳng bờ AB).Một đường thẳng qua A cắt (O) và (O') lần lượt tại C,D (A nằm giữa C và D).Các tiếp tuyến tại C của (O) và tại D của (O') cắt nhau tại K. Nối KB cắt CD tại I. Kẻ EI//DK (E∈BD).Chứng minh:

1.△BOO' Đồng dạng △BCD.

2.Tứ giác BCKD nội tiếp.

3.∠EAB=∠ACB.

Theo dõi (0) 1 Trả lời
Chứng minh rằng BDCO nội tiếp

bởi Chai Chai 25/01/2019

cho tam giác ABC có 3 góc nhọn nội tiếp trong (O). tiếp tuyến tại B và C của đường tròn cắt nhau tại D, từ D kẻ đường thẳng song song với AB, đường nayfcatws đường tròn ở E và F, cắt AC ở I.

c/m BDCO nội tiếp

c/m DOIC nội tiếp

c/m I là trung điểm của FE

Theo dõi (0) 1 Trả lời
Chứng minh rằng tứ giác AONE nội tiếp

bởi thúy ngọc 25/01/2019

Cho (O ;R) .Điểm M nằm ngoài đường tròn .Vẽ hai tiếp tuyến MA ;MB với đường tròn . Trên cung AB nhỏ lấy điểm N và từ N kẻ tiếp tuyến với đường tròn tại N cắ MA ;MB tại E và F

a) Cm: tứ giác AONE nội tiếp

b) Cm: Chu vi tam giác MEF và độ lớn góc EOF không phụ thuộc vào vị trí của N

c) Gọi I ;K lần lượt là giao điểm của OE ;OF với AB .Cho góc AOB = 120 độ .Tính EF/IK

d)Đường thẳng vuông góc với OM cắt MA ;MB lần lượt tại C ,D .Tìm vị trí của N để EC+FD có độ dài nhỏ nhất

Theo dõi (0) 1 Trả lời
Chứng minh N,D,P thẳng hàng

bởi minh thuận 25/01/2019

Cho $\Delta MNP$cân tại M. Vẽ đường tròn (O) đường kính MN, đường tròn (O') đường kính MP cắt nhau tại D

a) CM: N,D,P thẳng hàng

b) So sánh cung nhỏ DN và DP

Theo dõi (0) 1 Trả lời
Chứng minh tứ giác ADHE là hình chữ nhật

bởi Tran Chau 26/01/2019

Cho tam giác ABC vuông tại A nội tiếp đường tròn tâm O. Kẻ đường cao AH. Đường tròn (I) đường kính AH cắt AB,AC và đường tròn (O) lần lượt ở D,E,F. AF cắt đường thẳng BC tại S. Chứng minh:

a) Tứ giác ADHE là hình chữ nhật

b) Tứ giác BDEC nội tiếp được đường tròn

c) Chứng minh OA $⊥$ DE và 3 điểm S,D,E thẳng hàng

Làm hộ mình phần b,c với ạ

Theo dõi (0) 1 Trả lời