Bài tập 3.11 tr 116 sách BT Toán lớp 9 Tập 2
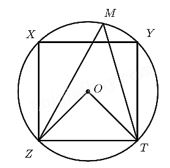
Hình vuông \(XYZT\) nội tiếp đường tròn tâm \(O\) bán kính \(R.\) điểm \(M\) bất kì thuộc cung nhỏ \(XT,\) \(\widehat {ZMT}\) có số đo bằng bao nhiêu\(?\)
\((A)\) \( 23^\circ30'; \)
\((B)\) \(45^\circ;\)
\((C)\) \(90^\circ;\)
\((D)\) Không tính được.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức: Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải chi tiết
Vì \(XYZT\) là hình vuông nên \(OT\bot OZ\), suy ra \(\widehat{ZOT}=90^0\)
Xét đường tròn \((O),\) ta có: \(\widehat{ZMT}=\dfrac{1}{2}\widehat{ZOT}\)\(=\dfrac{1}{2}.90^\circ=45^\circ\) (số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung)
Vậy chọn \((B)\) \(45^\circ\)
-- Mod Toán 9 HỌC247
-
Chứng minh tứ giác CKID nội tiếp được và IK // AB
bởi hà trang
22/02/2019
Cho tứ giác ABCD nội tiếp đường tròn (O; R) (AB < CD). Gọi P là điểm chính giữa của cung nhỏ AB; DP cắt AB tại E và cắt CB tại K; CP cắt AB tại F và cắt DA tại I.
a. Chứng minh: Tứ giác CKID nội tiếp được và IK // AB.
b. Chứng minh: AP2 = PE .PD = PF . PC
c. Chứng minh: AP là tiếp tuyến của đường tròn ngoại tiếp tam giác AED.
d. Gọi R1, R2 là các bán kính đường tròn ngoại tiếp các tam giác AED và BED.
Chứng minh:
R1+R2=\(\sqrt{4R^2-PA^2}\)
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC có 3 góc nhọn. Xác định vị tri của điểm M trong tam giác sao cho MA+MB+MC nhỏ nhất.
Theo dõi (0) 1 Trả lời -
cho đường tròn ( O ; R ) và 1 điểm P cố định ở bên trong đường tròn đó . 2 dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau : a) chứng minh rằng AB2 + CD2 không đổi ; b) chứng minh rằng PA2 + PB2 + PC2 + PD2 không phụ thuộc vào vị trí của điểm P .
Theo dõi (0) 1 Trả lời -
Tìm quỹ tích điểm I khi d quay quanh A biết tam giác ABC vuông tại A
bởi Nguyễn Quỳnh Anh
21/11/2017
Giúp e với ạ
.jpg)
Theo dõi (0) 2 Trả lời
