Bài tập 89 tr 104 sách GK Toán lớp 9 Tập 2
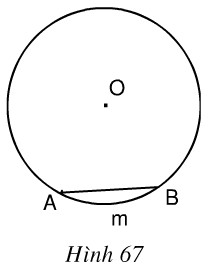
Trong hình 67, cung \(AmB\) có số đo là \(66^0\). Hãy:
a) Vẽ góc ở tâm chắn cung \(AmB\). Tính góc \(AOB\).
b) Vẽ góc nội tiếp đỉnh \(C\) chắn cung \(AmB\). Tính góc \(ACB\).
c) Vẽ góc tạo bởi tia tiếp tuyến \(Bt\) và dây cung \(BA\). Tính góc \(ABt\).
d) Vẽ góc \(ADB\) có đỉnh \(D\) ở bên trong đường tròn. So sánh \(\widehat {A{\rm{D}}B}\) với \(\widehat {ACB}\) .
e) Vẽ góc \(AEB\) có đỉnh \(E\) ở bên ngoài đường tròn (\(E\) và \(C\) cùng phía đối với \(AB\)). So sánh \(\widehat {A{\rm{E}}B}\) với \(\widehat {ACB}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn. Số đo góc ở tâm bằng số đo cung bị chắn.
- Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn. Số đo góc nội tiếp bằng nửa số đo cung bị chắn
- Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh tại tiếp điểm, một cạnh là tia tiếp tuyến và cạnh kia chứa dây cung. Số đo góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.
- Góc có đỉnh bên trong và bên ngoài đường tròn (xem lại SGK toán 9 tập 2 trang 80). Số đo góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn, số đo góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Lời giải chi tiết
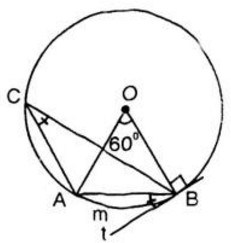
a) Từ \(O\) nối với hai đầu mút của cung \(AB\)
Ta có \(\widehat {AOB}\) là góc ở tâm chắn cung \(AB\)
Vì \(\widehat {AOB}\) là góc ở tân chắn cung \(AB\) nên
\(\widehat {AOB}\) =\(sđ\overparen{AmB}=60^0\)
b) Lấy một điểm \(C\) bất kì trên \((O)\). Nối \(C\) với hai đầu mút của cung \(AmB\). Ta được góc nội tiếp \(\widehat {ACB}\)
Khi đó: \(\widehat {ACB} = {1 \over 2}sđ\overparen{AmB}={1 \over 2}{60^0} = 30\)
c) Vẽ bán kính \(OB\). Qua \(B\) vẽ \(Bt\bot OB\). Ta được góc \(ABt\) là góc tạo bởi tia tiếp tuyến \(Bt\) với dây cung \(BA\).
Ta có: \(\widehat {ABt} = {1 \over 2}sđ\overparen{AmB} = {30^0}\)
d) Lấy điểm \(D\) bất kì ở bên trong đường tròn \((O)\). Nối \(D\) với \(A\) và \(D\) với \(B\). ta được góc là góc ở bên trong đường tròn \((O)\)
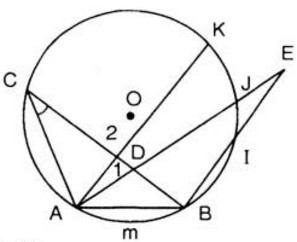
Ta có:
\(\eqalign{
& \widehat {ACB} = {1 \over 2}sđ\overparen{AmB}\cr
& \widehat {A{\rm{D}}B} = {1 \over 2}\left( sđ\overparen{AmB}+ sđ\overparen{CK} \right) \cr} \)
Mà \(sđ\overparen{AmB}+sđ\overparen{CK}>sđ\overparen{AmB}\)(do \(sđ\overparen{CK}>0\)) nên \(\widehat {A{\rm{D}}B} > \widehat {ACB}\)
e) Lấy điểm \(E\) bất kì ở bên ngoài đường tròn, nối \(E\) với \(A\) và \(E\) với \(B\), chúng cắt đường tròn lần lượt tại \(J\) và \(I\).
Ta có góc \(AEB\) là góc ở bên ngoài đường tròn \((O)\)
Có:
\(\eqalign{
& \widehat {ACB} = {1 \over 2}sđ\overparen{AmB} \cr
& \widehat {A{\rm{E}}B} = {1 \over 2}\left( sđ\overparen{AmB} - sđ\overparen{IJ} \right) \cr}\)
Mà \(sđ\overparen{AmB}\)– \(sđ \overparen{IJ}< sđ\overparen{AmB}\) (do \(sđ\overparen{IJ}> 0\))
Nên \(\widehat {A{\rm{E}}B} < \widehat {ACB}\).
-- Mod Toán 9 HỌC247
-


Từ điểm A nằm ngoài ( O:R) sao cho OA=2R, kẻ tiếp 2 tiếp tuyến AB và AC ( B,C thuộc đường tròn O). Chứng minh tam giác ABC đều
bởi Phamj Anh
 30/07/2022
30/07/2022
Từ điểm A nằm ngoài ( O:R) sao cho OA=2R, kẻ 2 tiếp tuyến AB và AC với ddongwf tròn ( B,C thuộc đường tròn O)
a) chứng minh tam giác ABC đều
b) tính góc BOCTheo dõi (0) 1 Trả lời -


Cho điểm M nằm bên ngoài đường tròn (O). Qua M kẻ hai tiếp tuyến MA, MB tới đường tròn (O), (A và B là các tiếp điểm), MO cát AB tại điểm H. Chứng minh tứ giác MAOB nội tiếp
bởi Giấu Tên
 02/05/2022
02/05/2022
Cho điểm M nằm bên ngoài đường tròn (O). Qua M kẻ hai tiếp tuyến MA, MB tới đường tròn (O), (A và B là các tiếp điểm), MO cát AB tại điểm H.
a) Chứng minh tứ giác MAOB nội tiếp,
b) Chứng minh
AH/OA = MA/MO
c) Gọi K là trung điểm của AH, Đường thẳng vuông góc với OK tại K. cắt tia MA tại điểm C và cắt MB tại điểm D. Chứng minh OCK = OBA và D là trung điểm của MB
Giúp mình với mình đang cần gấp
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC). Đường tròn đường kính AH cắt cạnh AB và AC theo thứ tự K và I. Chứng minh: AH=IK.
bởi Đinh Thị Thu Hiền
 24/03/2022
24/03/2022
Cho tam giác ABC vuông tại A,đường cao AH (H thuộc BC).Đường tròn đường kính AH cắt cạnh AB và AC theo thứ tự K và I
a Cm AH=IK
b tứ giác BKIC nội tiếp
c Qua A kẻ đường thẳng vuông góc với Ik cắt BC tại M.tính độ dài đoạn thẳng AM biết AB=3 cm,AC=4 cm
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông tại A, có AB =6 cm và AC = 8 cm. Tính độ dài đường cao AH và trung tuyến AM của tam giác ABC.
bởi Đặng Vân Hà Hà
 30/12/2021
30/12/2021
Câu hỏi:
Cho tam giác ABC vuông tại A, có AB =6 cm và AC = 8 cm.
a) Tính độ dài đường cao AH và trung tuyến AM của tam giác ABC.
b) Xác định tâm I và tính bán kính R của đường tròn đường kính HC.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có đường cao CH, biết BC= 6 cm, góc B có số đo 60 độ và góc C có số đo 40 độ. Tính độ dài đoạn thẳng CH, HB, CA. (làm tròn đến chữ số thập phân thứ 3).
bởi Lâm Quỳnh
 18/10/2021
18/10/2021
Cho tam giác ABC có đường cao CH, biết BC= 6 cm, góc B có số đo 60 và góc C có số đo 40
. a) Tính độ dài đoạn thẳng CH, HB, CA. (làm tròn đến chữ số thập phân thứ 3)
. b) Gọi M và N lần lượt là hình chiếu của H trên cạnh BC, AC. Chứng minh CN.AC = CM. BC
Theo dõi (0) 0 Trả lời -


Cho ∆ABC nhọn có các đường cao BE, CF cắt nhau ở H. Chứng minh 4 điểm B, F, E, C cùng thuộc một đường tròn; xác định tâm O của đường tròn đó.
bởi Trần Uyên
 26/08/2021
26/08/2021
Bài 4. Cho ∆ABC nhọn có các đường cao BE, CF cắt nhau ở H
a) Chứng minh 4 điểm B, F, E, C cùng thuộc một đường tròn; xác định tâm O của đường tròn đó
b) Chứng minh EF < BC
c) Gọi O’ là tâm của đường tròn ngoại tiếp ∆AEH. Chứng minh: OO’ vuông góc EF
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 88 trang 103 SGK Toán 9 Tập 2
Bài tập 90 trang 104 SGK Toán 9 Tập 2
Bài tập 91 trang 104 SGK Toán 9 Tập 2
Bài tập 92 trang 104 SGK Toán 9 Tập 2
Bài tập 93 trang 104 SGK Toán 9 Tập 2
Bài tập 94 trang 105 SGK Toán 9 Tập 2
Bài tập 95 trang 105 SGK Toán 9 Tập 2
Bài tập 96 trang 105 SGK Toán 9 Tập 2
Bài tập 97 trang 105 SGK Toán 9 Tập 2
Bài tập 98 trang 105 SGK Toán 9 Tập 2
Bài tập 99 trang 105 SGK Toán 9 Tập 2
Bài tập 73 trang 113 SBT Toán 9 Tập 2
Bài tập 74 trang 114 SBT Toán 9 Tập 2
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 77 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





