Bài tập 95 tr 105 sách GK Toán lớp 9 Tập 2
Các đường cao hạ từ \(A\) và \(B\) của tam giác \(ABC\) cắt nhau tại \(H\) (góc \(C\) khác \(90^0\)) và cắt đường tròn ngoại tiếp tam giác \(ABC\) lần lượt tại \(D\) và \(E\). Chứng minh rằng:
a) \(CD = CE\) ;
b) \(ΔBHD\) cân ;
c) \(CD = CH\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) Sử dụng: “Hai góc nội tiếp cùng chắn một cung thì bằng nhau” và hai góc phụ nhau từ đó suy ra hai cung bằng nhau và hai dây bằng nhau.
b) Chứng minh tam giác BHD có BK vừa là đường cao vừa là đường phân giác nên nó là tam giác cân
c) Sử dụng tính chất đường trung trực của đoạn thẳng
Lời giải chi tiết
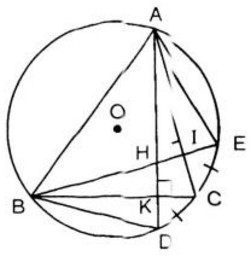
Ta có: \(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}B}\) (cùng chắn cung \(AB\))
\( \Rightarrow \widehat {CB{\rm{D}}} = \widehat {CA{\rm{E}}}\) (cùng phụ với hai góc bằng nhau)
⇒ \(sđ\overparen{CD}\)= \(sđ\overparen{CE}\)
Suy ra \(CD = CE\)
b) Ta có \(\widehat {EBC}\) và \(\widehat {CB{\rm{D}}}\) là góc nội tiếp trong đường tròn \(O\) nên :
\(\widehat {EBC} = {1 \over 2} sđ\overparen{CE}\) và \(\widehat {CB{\rm{D}}} = {1 \over 2}sđ\overparen{CD}\)
Mà \(sđ\overparen{CD}\)= \(sđ\overparen{CE}\)
nên \(\widehat {EBC} = \widehat {CB{\rm{D}}}\)
Vậy \(∆BHD\) cân tại \(B\)
c) Vì \(∆BHD\) cân và \(BK\) là đường cao cũng là đường trung trực của \(HD\). Điểm \(C\) nằm trên đường trung trực của \(HD\) nên \(CH = CD\)
-- Mod Toán 9 HỌC247
-


Chứng minh: NF×ME=NE×MF và MN là tiếp tuyến (I) tại N?
bởi Kiều Linh
 09/06/2020
09/06/2020
Cho tam giác ABC nhọn nội tiếp (O).Vẽ 3 đường cao AD,BE,CF cắt nhau tại H. Gọi I tâm đường tròn ngoại tiếp tứ giác BCEF .Gọi N là giao điểm của AD và EF ,M là giao điểm của EF và BC .
Chứng minh: NF×ME=NE×MF và MN là tiếp tuyến (I) tại N
Theo dõi (0) 0 Trả lời -


Chứng minh rằng khi điểm M di động trên cung nhỏ AC thì đường thẳng HK luôn đi qua một điểm cố định?
bởi TÔ NGỌC BẢO LINH
 07/06/2020
07/06/2020
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O trên cung nhỏ AC lấy điểm M Vẽ đường kính MN của đường tròn tâm O và O gọi H, K lần lượt là hình chiếu của điểm A trên BM và MN Chứng minh rằng khi điểm M di động trên cung nhỏ AC thì đường thẳng HK luôn đi qua một điểm cố định.
Theo dõi (0) 0 Trả lời -


Chứng minh tứ giác BCDE nội tiếp đường tròn tâm O?
bởi Thương Thương
 04/06/2020
04/06/2020
Cho tam giác ABC nhọn nội tiếp (O). Các đường cao BD và CE của tam giác cắt nhau tại H.
a) CM: tứ giác BCDE nội tiếp đường tròn tâm O.
b) Kẻ đường kình AK. CM: AB.BC = AK.BD.
c) CM: góc BCD = góc AED
d) Từ O kẻ OM vuông góc BC. CM: H, M, K thẳng hàng.
Theo dõi (0) 0 Trả lời -


Chứng minh rằng SH=SB=SC?
bởi Noob Ban
 04/06/2020
04/06/2020
Cho tam giác ABC nội tiếp đường trong (O).H là trực tâm tam giác ABC.Lấy S là điểm chính giữa cung BC không chứa điểm A.CMR SH=SB=SC
Theo dõi (0) 0 Trả lời -


Chứng minh : Tứ giác BNMC nội tiếp đường tròn, xác định tâm O của đường tròn đó?
bởi Thái Hoàng Nhi
 03/06/2020
03/06/2020
Bài 19: Cho tam giác ABC nhọn. Hai đường cao BM, CN của ta giác cắt nhau tại H
a/ Chứng minh : Tứ giác BNMC nội tiếp đường tròn, xác định tâm O của đường tròn đó
b/ Chứng minh : AB.NM = AM.BC
c/ Cho biết MC = R, BC = 2R. Tính diện tích hình quạt tròn giới hạn bởi cung nhỏ MC, bán kính OC, bán kính OM của (O) theo R.
d/ Gọi K là giao điểm của AH và BC. I là giao điểm của tia NK và (O).
Chứng minh : IM vuông góc BC
Theo dõi (0) 0 Trả lời -


Chứng minh A, H, O thẳng hàng?
bởi Nguyễn Thị Trà My
 02/06/2020
02/06/2020
cho đg tròn (O) và điểm A nằm ngoài đg tròn ,kẻ tiếp tuyến AB ,AC ,H là trung điểm BC
a) c/m A, H, O thẳng hàng.
b) đg kính BD và CK guông góc BD tại K
c/m AC.CD=Ck.AO .c) AO cắt đg tròn tại M,N c/m HM.AN=AM.HN
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 93 trang 104 SGK Toán 9 Tập 2
Bài tập 94 trang 105 SGK Toán 9 Tập 2
Bài tập 96 trang 105 SGK Toán 9 Tập 2
Bài tập 97 trang 105 SGK Toán 9 Tập 2
Bài tập 98 trang 105 SGK Toán 9 Tập 2
Bài tập 99 trang 105 SGK Toán 9 Tập 2
Bài tập 73 trang 113 SBT Toán 9 Tập 2
Bài tập 74 trang 114 SBT Toán 9 Tập 2
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 77 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





