Bài tập 73 tr 113 sách BT Toán lớp 9 Tập 2
Cho đường tròn đường kính \(AB.\) Qua \(A\) và \(B\) kẻ hai tiếp tuyến của đường tròn đó. Gọi \(M\) là một điểm trên đường tròn. Các đường thẳng \(AM\) và \(BM\) cắt các tiếp tuyến trên lần lượt tại \(B’\) và \(A’.\)
\(a)\) Chứng minh rằng \({\rm{AA}}'.BB' = A{B^2}\)
\(b)\) Chứng minh rằng \(A'{A^2} = A'M.A'B\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Nếu hai tam giác đồng dạng ta suy ra các cạnh tương ứng tỉ lệ.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng tích cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Lời giải chi tiết
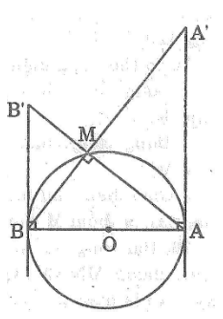
\(a)\) Xét \(∆AA'B\) và \(∆BB'A:\)
\(\widehat {A'AB} = \widehat {B'BA} = {90^0}\)
\(\widehat {BB'A} = \widehat {ABA'}\) (vì cùng phụ với \(\widehat {BAB'}\))
Suy ra: \(∆AA'B\) đồng dạng \(∆BAB'\; (g.g)\)
\(\displaystyle {{AA'} \over {BA}} = {{AB} \over {BB}} \Rightarrow AA'.BB' = A{B^2}\)
\(b)\) \(\widehat {AMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow AM \bot A'B\)
\(∆AA'B\) vuông tại \(A.\) Theo hệ thức lượng trong tam giác vuông ta có:
\(AA{'^2} = A'M.A'B\)
-- Mod Toán 9 HỌC247
-


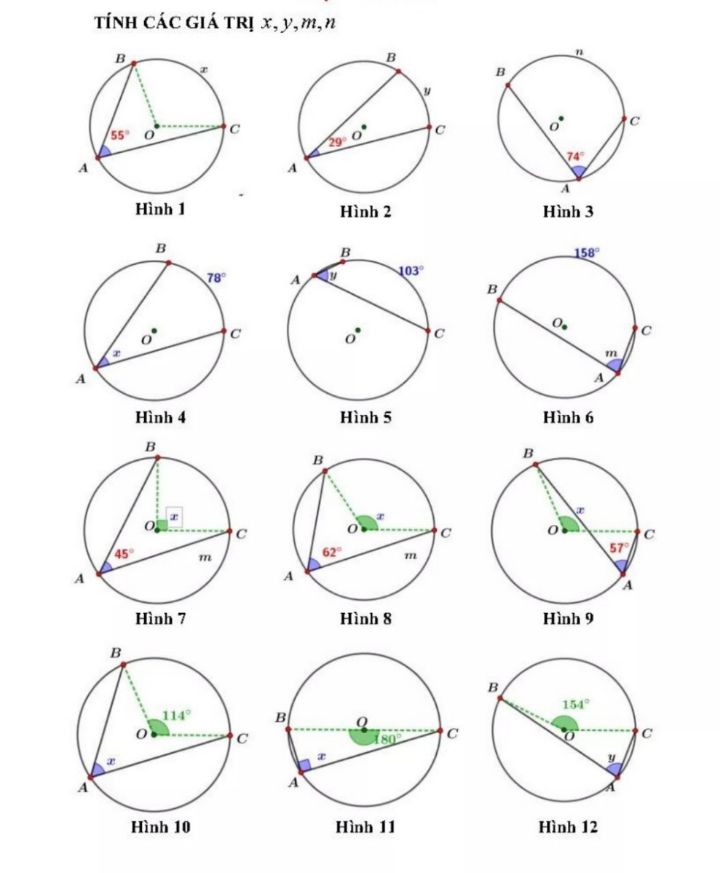
Tính các giá trị x, y, m, n?
bởi Thiên Dii
 16/04/2020
16/04/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Cho (O; R). Dây cung AB. Gọi I là trung điểm AB biết: R=15cm, OI=6cm.Tính độ dài dây AB.
bởi Thu Võ
 01/04/2020
01/04/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Giải giúp mình.
Bài 1: Cho tam giác AOB=60 độ trong (O;R). Tính số đo cung nhỏ AB
Bài 2 : Cho góc BAC = 30 độ là góc nội tiếp chắn cung BC trong (O ; R). Tính số đo cung nhỏ BC.
Bài 3 : Cho hình vẽ a). Biết góc AEC= 40 độ. Tính tổng số đo của cung AC và cung BD.
Bài 4 : Cho hình vẽ . Biết góc AIC= 20 độ. Tính sđ AC - sđ BD ?
Bài 5 : Cho hình vẽ . Biết góc xAB = 45 độ. Tính số đo cung nhỏ AB ?
Bài 6 : Cho tứ giác ABCD nội tiếp (O ; R) và có Â = 80 độ. Vậy số đo góc
bằng bao nhiêu ?
Bài 7: Cho đường tròn (O;R) vẽ góc BAC có số đo bằng 30 độ
a/ Tính số đo cung BC
b/ Tính độ dài dây BC và độ dài cung BC theo R
c/ Tính diện tích hình quạt ứng với góc ở tâm BOC theo R
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R). Ba đường cao AD, BE, CF cắt nhau tại H. Chứng minh tứ giác AEHF là tứ giác nội tiếp.
bởi Tự Tâm
 24/03/2020
Giúp em với
24/03/2020
Giúp em với Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho đường tròn (O;R), M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn tại hai điểm C và D (C nằm giữa M và D). Gọi I là trung điểm day CD, kẻ AH vuông góc MO tại H. Tính OH, OM theo R.
bởi Minh Nguyen
 23/03/2020
23/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R), tia phân giác BAC cắt BC tại D, cắt (O) tại E. Vẽ DK vuoog AB tại K và DM vuông AC tại M. Chứng minh AKDM nội tiếp.
bởi Nguyễn Hoàng
 11/03/2020
11/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 98 trang 105 SGK Toán 9 Tập 2
Bài tập 99 trang 105 SGK Toán 9 Tập 2
Bài tập 74 trang 114 SBT Toán 9 Tập 2
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 77 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





