Bài tập 3.12 tr 116 sách BT Toán lớp 9 Tập 2
Cho hình như hình bên \((PQ = PR;\) \(QY\) và \(RX\) là các tia phân giác\().\) Khi đó, \(PYKX\) là:
\((A)\) hình thang và không phải là hình bình hành.
\((B)\) hình bình hành và không phải hình thoi.
\((C)\) hình thoi và không phải hình chữ nhật.
\((D)\) hình chữ nhật.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Tứ giác có các góc đối bằng nhau là hình bình hành.
+) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
+) Hình chữ nhật là tứ giác có \(4\) góc vuông.
Lời giải chi tiết
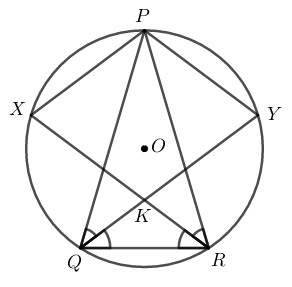
Ta có: \(PQ=PR\) (gt) nên tam giác \(PQR\) cân tại P
Suy ra \( \widehat{PQR}=\widehat{PRQ}\)
Mà \(QY,RX\) lần lượt là tia phân giác của các góc \( \widehat{PQR},\widehat{PRQ}\)
Nên \( \widehat{PQY}=\widehat{YQR}\)\(= \widehat{QRX}=\widehat{XRP}\)
Suy ra các cung \(PX,PY,QX,RY\) bằng nhau (các góc nội tiếp bằng nhau chắn các cung bằng nhau)
Suy ra \( \widehat{PRX}=\widehat{RPY}\) (hai góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Mà hai góc ở vị trí so le trong nên \(XR//PY\)
Lại có \( \widehat{PQY}=\widehat{XPQ}\) (hai góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Mà hai góc ở vị trí so le trong nên \(PX//QY\)
Suy ra tứ giác \(PXKY\) là hình bình hành.
Mà \(PX=PY\) (do cung PX bằng cung PY) nên \(PXKY\) là hình thoi.
Mặt khác: \(\widehat{PXR}\ne 90^\circ\) (vì \(PQ\) không phải đường kính)
Do đó: tứ giác \(PXKY\) là hình thoi nhưng không phải hình chữ nhật.
Vậy chọn \((C)\) hình thoi và không phải hình chữ nhật.
-- Mod Toán 9 HỌC247
-


Chứng minh tứ giác CKID nội tiếp được và IK // AB
bởi hà trang
 22/02/2019
22/02/2019
Cho tứ giác ABCD nội tiếp đường tròn (O; R) (AB < CD). Gọi P là điểm chính giữa của cung nhỏ AB; DP cắt AB tại E và cắt CB tại K; CP cắt AB tại F và cắt DA tại I.
a. Chứng minh: Tứ giác CKID nội tiếp được và IK // AB.
b. Chứng minh: AP2 = PE .PD = PF . PC
c. Chứng minh: AP là tiếp tuyến của đường tròn ngoại tiếp tam giác AED.
d. Gọi R1, R2 là các bán kính đường tròn ngoại tiếp các tam giác AED và BED.
Chứng minh:
R1+R2=\(\sqrt{4R^2-PA^2}\)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có 3 góc nhọn. Xác định vị tri của điểm M trong tam giác sao cho MA+MB+MC nhỏ nhất.
Theo dõi (0) 1 Trả lời -


cho đường tròn ( O ; R ) và 1 điểm P cố định ở bên trong đường tròn đó . 2 dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau : a) chứng minh rằng AB2 + CD2 không đổi ; b) chứng minh rằng PA2 + PB2 + PC2 + PD2 không phụ thuộc vào vị trí của điểm P .
Theo dõi (0) 1 Trả lời -


Tìm quỹ tích điểm I khi d quay quanh A biết tam giác ABC vuông tại A
bởi Nguyễn Quỳnh Anh
 21/11/2017
21/11/2017
Giúp e với ạ
.jpg) Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời






