Bài tập 91 tr 104 sách GK Toán lớp 9 Tập 2
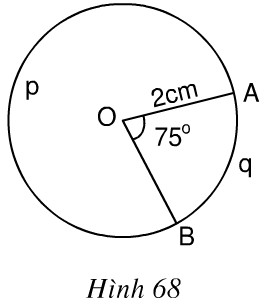
Trong hình 68, đường tròn tâm O có bán kính \(R = 2cm\), góc \(AOB = 75^0\).
a) Tính số đo cung \(ApB\).
b) Tính độ dài hai cung \(AqB\) và \(ApB\).
c) Tính diện tích hình quạt tròn \(OAqB\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Trên đường tròn bán kính R, độ dài l của 1 cung \({n^0}\) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\)
+) Diện tích hình quạt tròn bán kính R, cung \({n^0}\) được tính theo công thức: \(S = \dfrac{{\pi {R^2}n}}{{360}}\left( {hay\,\,S = \dfrac{{lR}}{2}} \right)\)
Lời giải chi tiết
a) Ta có \(\widehat {AOB}\) là góc ở tâm chắn cung \(AqB\) nên:
\(\widehat {AOB}\) = \(sđ\overparen{AqB}\) hay \(sđ\overparen{AqB}=75^0\)
Vậy \(sđ\overparen{ApB}\) \(=360°- \overparen{AqB}\) \(=360^0 - 75^0 = 285^0\)
b) \({l_{\overparen{AqB}}}\) là độ dài cung \(AqB\), ta có:
\(\displaystyle {l_{\overparen{AqB}}}\) \(=\displaystyle {{\pi Rn} \over {180}} = {{\pi .2.75} \over {180}} = {5 \over 6}\pi (cm)\)
Gọi \({l_{\overparen{ApB}}}\) là độ dài cung \(ApB\) ta có:
\(\displaystyle {l_{\overparen{ApB}}}= {{\pi Rn} \over {180}} = {{\pi .2.285} \over {180}} = {{19\pi } \over 6}(cm)\)
c) Diện tích hình quạt tròn \(OAqB\) là: \(\displaystyle {S_{OAqB}} = {{\pi {R^2}n} \over {360}} = {{\pi {2^2}.75} \over {360}} = {{5\pi } \over 6}(c{m^2})\)
-- Mod Toán 9 HỌC247
-


Biết nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba bạn Bình cần đặt một thang đi lên gác, biết khi đặt thang phải để thang tạo được với mặt đất một góc \({70^o}\)thì đảm bảo sự an toàn khi sử dụng. Với kiến thức đã học, Bình hãy giúp Ba tính chiều dài thang là bao nhiêu mét để sử dụng. (kết quả làm tròn đến chữ số thập phân thứ nhất)
bởi Nguyễn Minh Hải
 09/07/2021
09/07/2021
Biết nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba bạn Bình cần đặt một thang đi lên gác, biết khi đặt thang phải để thang tạo được với mặt đất một góc \({70^o}\)thì đảm bảo sự an toàn khi sử dụng. Với kiến thức đã học, Bình hãy giúp Ba tính chiều dài thang là bao nhiêu mét để sử dụng. (kết quả làm tròn đến chữ số thập phân thứ nhất)
Theo dõi (0) 1 Trả lời -


Từ điểm A ở bên ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB, AC của (O) với B,C là hai tiếp điểm Cho điểm P thuộc cung lớn BC của (O) . Kẻ PE vuông AB, PF vuông AC, PQ vuông BC.
bởi Thanh Thien
 16/05/2021
Chứng minh PQ^2=PE.PFTheo dõi (0) 0 Trả lời
16/05/2021
Chứng minh PQ^2=PE.PFTheo dõi (0) 0 Trả lời -


Từ điểm M nằm ngoài đường tròn (O,R) vẽ tiếp tuyến MA và cát tuyến MBC. Đường cao AD, CE trong tam giác ABC cắt nhau tại H. N là trung điểm của BC. Chứng minh BH vuông với AC và tứ giác BEHD nội tiếp)
bởi Soda Sữa
 18/04/2021
Từ điểm M nằm ngoài đường tròn (O,R) vẽ tiếp tuyến MA và cát tuyến MBC. Đường cao AD, CE trong tam giác ABC cắt nhau tại H. N là trung điểm của BC. a) Chứng minh BH vuông với AC và tứ giác BEHD nội tiếpb) Chứng minh MA²= MB.MC. c) Kéo dài AN cắt (O) tại F. So sánh NF và NHTheo dõi (0) 0 Trả lời
18/04/2021
Từ điểm M nằm ngoài đường tròn (O,R) vẽ tiếp tuyến MA và cát tuyến MBC. Đường cao AD, CE trong tam giác ABC cắt nhau tại H. N là trung điểm của BC. a) Chứng minh BH vuông với AC và tứ giác BEHD nội tiếpb) Chứng minh MA²= MB.MC. c) Kéo dài AN cắt (O) tại F. So sánh NF và NHTheo dõi (0) 0 Trả lời -


Cho 2 đường thẳng (O;R) và (O;R') tiếp xúc ngoài tại A (R>R'). Vẽ các đường kính AOB, AO'C. Dây cung DE của (O) vuông góc với BC tại trung điểm K của BC. Chứng minh rằng: BAE = BDE
bởi Thiên Thiên
 10/04/2021
10/04/2021
Cho 2 đường thẳng (O;R) và (O;R') tiếp xúc ngoài tại A (R>R'). Vẽ các đường kính AOB, AO'C. Dây cung DE của (O) vuông góc với BC tại trung điểm K của BC.
a) Chứng minh rằng: BAE = BDE
b) Tứ giác BDCE là hình gì? Vì sao?
c) Gọi I là giao điểm của DA với (O'). Chứng minh rằng: 3 điểm C,I,E thẳng hàng
d) Chứng minh rằng: KI là tiếp tuyến của (O')
Theo dõi (0) 1 Trả lời -


Cho đường tròn(O,R) và từ điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với(O) (B,C là các tiếp diễm). Gọi H là giao điểm củaOA và BC. chứng minh: bốn điểm A,B,O,C cùng thuộc một đường tròn.
bởi Vũ Việt Thành
 08/01/2021
08/01/2021
C1:Cho đường tròn(O,R) và từ điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với(O) (B,C là các tiếp diễm ). Gọi H là giao điểm củaOA và BC.
a) chứng minh: bốn điểm A,B,O,C cùng thuộc một đường tròn.
b) chứng minh: OA là đường trung trực của BC
c) lấy D là điểm đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với (D).chứng minh:DE BD BE BA=
d) tính số do góc HEC.
Theo dõi (0) 1 Trả lời -


Chứng minh điểm N thuộc một đường tròn cố định khi A di động trên cung lớn BC?
bởi Trương Trang
 26/08/2020
26/08/2020
Cho đường tròn (O;R) và dây BC không đi qua tâm. Điểm A di dộng trên cung lớn BC. Gọi M là trung điểm AC, N là hình chiếu của M trên AB. Chứng minh điểm N thuộc một đường tròn cố định khi A di động trên cung lớn BC.
Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 89 trang 104 SGK Toán 9 Tập 2
Bài tập 90 trang 104 SGK Toán 9 Tập 2
Bài tập 92 trang 104 SGK Toán 9 Tập 2
Bài tập 93 trang 104 SGK Toán 9 Tập 2
Bài tập 94 trang 105 SGK Toán 9 Tập 2
Bài tập 95 trang 105 SGK Toán 9 Tập 2
Bài tập 96 trang 105 SGK Toán 9 Tập 2
Bài tập 97 trang 105 SGK Toán 9 Tập 2
Bài tập 98 trang 105 SGK Toán 9 Tập 2
Bài tập 99 trang 105 SGK Toán 9 Tập 2
Bài tập 73 trang 113 SBT Toán 9 Tập 2
Bài tập 74 trang 114 SBT Toán 9 Tập 2
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 77 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





