Bài tập 77 tr 114 sách BT Toán lớp 9 Tập 2
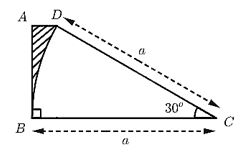
Tính diện tích phần gạch sọc trên hình sau (theo kích thước đã cho trên hình)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng cạnh huyền nhân với \(\sin\) góc đối hoặc \(\cos\) góc kề.
+) Diện tích hình thang bằng nửa tổng hai đáy nhân với chiều cao.
+) Diện tích hình quạt tròn bán kính \(R,\) cung \(n^\circ\) được tính theo công thức: \(S=\dfrac{\pi R^2n}{360}.\)
Lời giải chi tiết
.jpg)
Diện tích phần gạch sọc là hiệu giữa diện tích hình thang \(ABCD\) và diện tích hình quạt tròn có góc ở tâm \(30^0\) của đường tròn bán kính bằng a.
Từ \(D\) kẻ \(DH \bot BC\), suy ra \(ADHB\) là hình chữ nhật.
Trong tam giác vuông \(HDC\) có \(\widehat {DHC} = {90^0}\)
\(DH = DC.\sin \widehat{C} = a.\sin {30^0} = \displaystyle{a \over 2}\)
\(CH = DC.\cos\widehat C = a.\cos{30^0} =\displaystyle {{a\sqrt 3 } \over 2}\)
\(BH = BC - HC = \displaystyle a - {{a\sqrt 3 } \over 2} \)\(= \displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2}\)
\( \Rightarrow AD =BH= \displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2}\) (do \(ADHB\) là hình chữ nhật)
Diện tích của hình thang \(ABCD\) bằng:
\(\displaystyle{{AD + BC} \over 2}.DH \)\(=\displaystyle{{\displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2} + a} \over 2}.{a \over 2}\)
\( = \displaystyle {{{a^2}\left( {4 - \sqrt 3 } \right)} \over 8}\)
Diện tích hình quạt tròn bằng: \(\displaystyle{{\pi .{a^2}.30} \over {360}} = {{\pi {a^2}} \over {12}}\)
Diện tích phần gạch sọc:
\(S = \displaystyle{{{a^2}\left( {4 - \sqrt 3 } \right)} \over 8} - {{\pi a} \over {12}}\)
\( = \displaystyle{{3{a^2}\left( {4 - \sqrt 3 } \right) - 2\pi {a^2}} \over {24}}\)
\( = \displaystyle{{{a^2}} \over {24}}\left( {12 - 3\sqrt 3 - 2\pi } \right)\)
-- Mod Toán 9 HỌC247
-


Cho tam giác ABC có AB = 2,345 cm; BC = 5,567cm; AC = 4,236cm, đường cao AH, trung tuyến AM.
a. Tính AH?
b. Tính AM?
Theo dõi (0) 2 Trả lời -


Chứng minh ab^2= ac.ad
bởi Nguyễn Vân
 07/01/2019
07/01/2019
Cho tam giác abc nhọn nội tiếp (o) (với ab<ac) qua a kẻ tiếp tuyến xy với (o). Từ b kẻ đường thảng // xy,cắt ac ở d. Cmr: ab2= ac.ad
Theo dõi (0) 1 Trả lời -


Chứng minh DM là phân giác góc ADE
bởi Phạm Khánh Ngọc
 09/01/2019
09/01/2019
Cho ∆ ABC vuông tại A ( AB<AC). Gọi M là trung điểm AC. Đường tròn đường kính MC cắt ở E và cắt đường thẳng BM tại D
a) ABCD nội tiếp (O) . Xác định O
b) chứng minh DM là phân giác góc ADE
c) OM là tiếp tuyến của đường tròn đường kính MC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có 3 góc nhọn ( AB>AC)nội tiếp đường tròn tâm (O;R).Vẽ đường cao AD , BE, CF cắt nhau tại H
a) gọi M là trung điểm BC. chứng minh EFMD nt
b) Qua D kẻ đtường thẳng song song EF cắt AB tại R, AC tại Q. EF cắt BC tại K. Chứng minh đtron ngoại tiếp tam giác KQR luôn đi qua M
c) giả sử \(S_{ABC}=1\), góc BAC=30 độ. Tính \(S_{BCEF}\)?
Theo dõi (0) 1 Trả lời -


Chứng minh rằng MC.OE=EM.OF
bởi Nguyễn Thị Lưu
 22/01/2019
22/01/2019
Cho (O) bán kính AB.Từ A và B kẻ 2 tiếp tuyến Ax, By.Từ 1 điểm C trên đường tròn(khác A và B).Kẻ tiếp tuyến thứ 3 cắt Ax tại E và By tại F.Gọi M là giao điểm của AC và EO,N là giao điểm của BC và OF. CMR :MC.OE=EM.OF
Theo dõi (0) 1 Trả lời -


Chứng minh rằng BC/MD=AC/ME+AB/MF
bởi Tieu Dong
 22/01/2019
22/01/2019
Cho tam giác ABC ( AB<AC) nội tiếp đường tròn tâm O. M là điểm nằm trên cung BC không chứa điểm A. Gọi D,E,F lần lượt là hình chiếu của M trên BC, CA, AB. C/m rằng
\(\dfrac{BC}{MD}=\dfrac{AC}{ME}+\dfrac{AB}{MF}\)
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





