Bài tập 78 trang 114 SBT Toán 9 Tập 2

31 BT SGK

Bài tập 78 tr 114 sách BT Toán lớp 9 Tập 2

Cho tam giác \(AHB\) có \(\widehat H = 90^\circ ,\widehat A = 30^\circ \) và \(BH = 4cm.\) Tia phân giác của góc \(B\) cắt \(AH\) tại \(O.\) Vẽ đường tròn \((O; OH)\) và đường tròn \((O; OA).\)

\(a)\) Chứng minh đường tròn \((O; OH)\) tiếp xúc với cạnh \(AB.\)

\(b)\) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên.

Hình học 9 Chương 3 Bài 11 Trắc nghiệm Hình học 9 Chương 3 Bài 11 Giải bài tập Hình học 9 Chương 3 Bài 11

Hướng dẫn giải chi tiết

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Tính chất tia phân giác của một góc: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.

+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với \(\tan\) góc đối.

+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh huyền nhân với \(\cos\) góc kề.

+) Diện tích \(S\) của một hình tròn bán kính \(R\) được tính theo công thức: \(S=\pi.R^2\).

Lời giải chi tiết

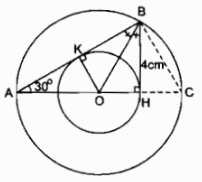
a) Kẻ \(OK \bot AB\)

BO là đường phân giác của \(\widehat B\)

\( \Rightarrow OK = OH\) (tính chất đường phân giác)

Vậy đường tròn (O; OH) tiếp xúc với AB tại K.

b) ∆AHB có \(\widehat H = {90^0}\); \(\widehat A = {30^0}\)

Suy ra: \(\widehat B = {60^0} \Rightarrow \widehat {ABO} = {1 \over 2}\widehat B = {30^0}\)

Suy ra: ∆OAB cân tại O nên OB = OA

Vậy B (O; OA)

∆BHO có \(\widehat H = {90^0}\); \(\widehat {OBH} = {30^0}\)

\(OH = BH.\tan {30^0} = 4.{{\sqrt 3 } \over 3} = {{4\sqrt 3 } \over 3}\) (cm)

\(OB = {{BH} \over {\cos \widehat {OBH}}} = {4 \over {\cos {{30}^0}}} = {4 \over {{{\sqrt 3 } \over 2}}} = {{8\sqrt 3 } \over 3}\) (cm)

Diện tích đường tròn nhỏ: S₁ = \(\pi {\left( {{{4\sqrt 3 } \over 3}} \right)^2} = {{16\pi } \over 3}\) (cm²)

Diện tích đường tròn lớn: \({S_2} = \pi {\left( {{{8\sqrt 3 } \over 3}} \right)^2} = {{64\pi } \over 3}\) (cm²)

Diện tích hình vành khăn:

S = \({S_2} - {S_1} = {{64\pi } \over 3} - {{16\pi } \over 3} = {{48\pi } \over 3} = 16\pi \) (cm²)

-- Mod Toán 9 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 78 trang 114 SBT Toán 9 Tập 2 HAY thì click chia sẻ

YOMEDIA

Chứng minh các tứ giác BFLK và CELK nội tiếp

bởi hi hi 22/01/2019

1.Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm tùy ý trên cạnh BC.

L là hình chiếu của H trên AK. Chứng minh các tứ giác BFLK và CELK nội tiếp

2.Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm tùy ý trên cạnh BC (K khác B, C, D).

Đường tròn ngoại tiếp tam giác CEK và tam giác BFK cắt nhau tại L.

a) Chứng minh A, L, K thẳng hàng

b) Chứng minh HL vuông góc với AK

3. Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm tùy ý trên cạnh BC (K khác B, C).

Kẻ đường kính KM của đường tròn ngoại tiếp tam giác BKF và đường kính KN của đường tròn ngoại tiếp tam giác CEK.

Chứng minh M, H, K thẳng hàng

4. Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm tùy ý trên cạnh BC (K khác B, C).

Đường tròn ngoại tiếp tam giác BKF và đường tròn ngoại tiếp tam giác CEK cắt nhau tại N.

Tìm vị trí của K trên BC để BC, EF, HL đồng quy.

Theo dõi (0) 2 Trả lời
Chứng minh góc EBF=ECF

bởi Lê Nhật Minh 22/01/2019

Cho tam giá ABC có 2 đường cao AD và BE cắt nhau tại điểm H. biết 3 góc CAB, góc ABC, góc BCA đều là góc nhọn. gọi F là giao điểm của 2 đường thẳng CH và AB.

1) Chứng minh tứ giác CDHE là tgnt đường tròn. xác định tâm của đường tròn ngoại tiếp tg CDHE

2) Chứng minh góc EBF=ECF

3) Tìm tâm của đường tròn nội tiếp tam giác DEF.

Theo dõi (0) 2 Trả lời
Chứng minh MN=BM+CN

bởi Nguyễn Trung Thành 22/01/2019

Cho nửa đường tròn tâm O đường kình BC. Vẽ 2 tiếp tuyến Bx và Cy của (O) gọi A là điểm trên nửa đường tròn sao cho AB<AC. Tiếp tuyến tại A của (O) cắt Bx và Cy tại M và N.

a, Chứng minh: MN=BM+CN

b, Chứng minh: OM vuông góc AB và OM song son với AC

Theo dõi (0) 2 Trả lời
Chứng minh rằng tứ giác BKHC nội tiếp

bởi thanh hằng 23/01/2019

Cho tam giác ABC có 3 góc nhọn nội tiếp ( O;R) . Đường cao BH và CK cắt (O) tại E và F. Chứng minh rằng

a, Tứ giác BKHC nội tiếp

b, OA \(\perp\)EF và EF//HK

c, Khi tam giác ABC đều có cạnh bằng β. Tính diện tích hình viên phân chắn cung nhỏ BC của (O)

Theo dõi (0) 1 Trả lời
Chứng minh rằng AB.AC=2R.AH

bởi Lê Nguyễn Hạ Anh 24/01/2019

Cho tam giác ABC nội tiếp (O); tiếp tuyến A của (O) cắt BC tại M. Từ A hạ đường cao vuông góc với BC tạ H

a, CMR: AB.AC=2R.AH

b, CMR; \(\dfrac{MB}{MC}=\left(\dfrac{AB}{AC}\right)^2\)

c, Cho N bất kì thuộc BC(N≠B≠C); EN⊥AB; NF⊥AC

Tìm vị trí của N sao cho EF đạt GTNN

Theo dõi (0) 1 Trả lời
Chứng minh rằng tứ giác BEFH nội tiếp

bởi minh thuận 24/01/2019

cho tam giác ABC nhọn nội tiếp đường tròn (O) bán kính R (AB>AC) gọi H là giao điểm 2 đường cao BD&CE của tam giác ABC.

a)CM:tứ giác BEFH nội tiếp

b) vẽ đường kính AI của đường tròn (O) gọi K là điểm đối xứng với H qua BC. CM: tứ giác BIKC là hình thang cân.

Theo dõi (0) 1 Trả lời