Bài tập 96 tr 105 sách GK Toán lớp 9 Tập 2
Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\) và tia phân giác của góc \(A\) cắt đường tròn tại \(M\). Vẽ đường cao \(AH\). Chứng minh rằng:
a) \(OM\) đi qua trung điểm của dây \(BC\).
b) \(AM\) là tia phân giác của góc \(OAH\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) + Sử dụng hai góc nội tiếp bằng nhau chắn hai cung bằng nhau
+ Chỉ ra M là điểm chính giữa cung BC.
b) + Chứng minh \(OM//AH\)
+ Sử dụng tính chất hai đường thẳng song song và tính chất tam giác cân.
Lời giải chi tiết
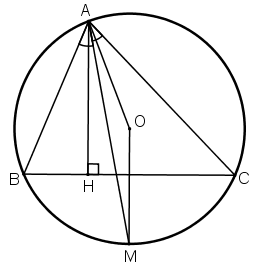
a) Vì \(AM\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAM} = \widehat {MAC}\)
Mà \(\widehat {BAM}\) và \(\widehat {MAC}\) đều là góc nội tiếp của \((O)\) nên
\(\overparen{BM}\)=\(\overparen{MC}\)
⇒ \(M\) là điểm chính giữa cung \(BC\)
Vậy \(OM \bot BC\) và \(OM\) đi qua trung điểm của \(BC\)
b) Ta có : \(OM \bot BC\) và \(AH\bot BC\) nên \(AH//OM\)
\( \Rightarrow \widehat {HAM} = \widehat {AM{\rm{O}}}\) (so le trong) (1)
Mà \(∆OAM\) cân tại \(O\) (do \(OA=OM\) (= bán kính đường tròn (O)) nên \(\widehat {AM{\rm{O}}} = \widehat {MAO}\) (2)
Từ (1) và (2) suy ra: \(\widehat {HA{\rm{M}}} = \widehat {MAO}\)
Vậy \(AM\) là đường phân giác của góc \(OAH\)
-- Mod Toán 9 HỌC247
-


Chứng minh tứ giác MAOB nội tiếp?
bởi Bạch Uyển Nhi
 31/05/2020
31/05/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Cho đường tròn (O) và điểm A nằm ngoài đtron từ A kẻ 2 tiếp tuyến AB và AC với dtron ( B, C là 2 tiếp điểm)
bởi mailananh
 30/05/2020
30/05/2020
Chứng minh:
a, tứ giác ABOC nội tiếp .
b, Gọi H làg trực tâm của tgiac ABC. Cm tg OBCH là hình thoi.
c, Gọi I là giao điểm của OA với đtron . Chứng minh I là tâm của dtron ngoại tiếp tam giác abc
Theo dõi (0) 0 Trả lời -


Chứng minh BNCO là tứ giác nội tiếp PO song song với BC?
bởi Hà Phạm
 29/05/2020
29/05/2020
cho đường tròn tâm o bán kính AB và điểm C nằm trên đường tròn đó qua B và C kẻ tuyết tuyến với đường tròn tại N đường thẳng CN cắt AB tại M phân giác góc MOC cắt MN tại P chứng minh BNCO là tứ giác nội tiếp PO song song với BC
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Từ một điểm A nằm ngoài đường tròn (O), vẽ 2 tiếp tuyến AB, AC và cát tuyến AMN của đường tròn đó. Cho góc BAC có số đo bằng 60 độ, OB = 2cm.
bởi Dương Hànn Dii
 28/05/2020
28/05/2020
a) Chứng minh tứ giác ABOC nội tiếp, xác định tâm của đường tròn ngoại tiếp tứ giác ABCO
b) Tính số đo của góc BOA
c) Tính diện tích hình quạt OBMC
Theo dõi (0) 0 Trả lời -


Chứng minh ABCD là một tứ giác nội tiếp?
bởi Nguyễn Xuân
 25/05/2020
25/05/2020
Giải bài 97 cho e vs ạ
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác AHC bằng bán kính đường tròn ngoại tiếp tam giác BHC?
bởi Tuyết Nguyễn
 24/05/2020
24/05/2020
Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90 độ) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác AHC bằng bán kính đường tròn ngoại tiếp tam giác BHC?
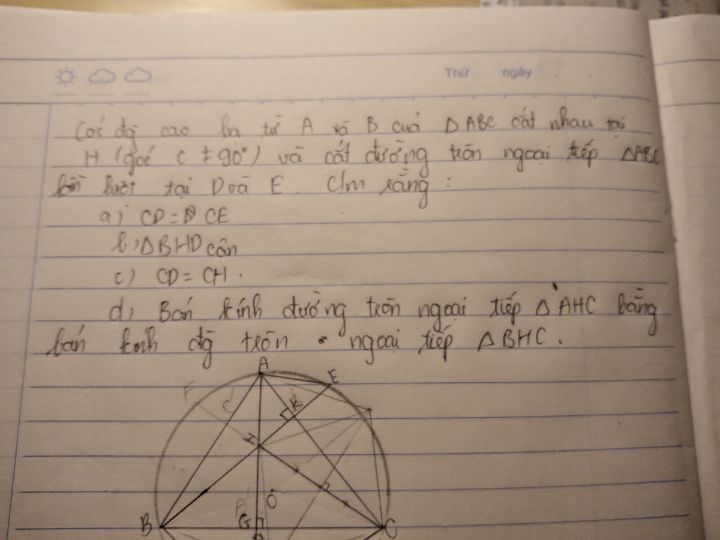 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 94 trang 105 SGK Toán 9 Tập 2
Bài tập 95 trang 105 SGK Toán 9 Tập 2
Bài tập 97 trang 105 SGK Toán 9 Tập 2
Bài tập 98 trang 105 SGK Toán 9 Tập 2
Bài tập 99 trang 105 SGK Toán 9 Tập 2
Bài tập 73 trang 113 SBT Toán 9 Tập 2
Bài tập 74 trang 114 SBT Toán 9 Tập 2
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 77 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





