Bài tập 3.9 tr 116 sách BT Toán lớp 9 Tập 2
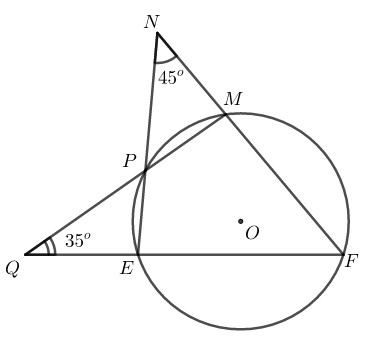
Cho hình sau. Khi đó, số đo của \(\widehat {MFE}\) bằng bao nhiêu\(?\)
\((A)\) \(50^\circ;\) \((B)\) \(80^\circ;\)
\((C)\) \(130^\circ;\) \( (D)\) Không tính được.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải chi tiết
Xé đường tròn \((O),\) ta có: \(\widehat{MFE}= \dfrac{1}{2}sđ\overparen{ME}(nhỏ)\) (góc nội tiếp)
\(=\dfrac{1}{2}(sđ \overparen{PM} +sđ \overparen{PE})\)
Ta có:
+) \(\widehat{N}=\dfrac{1}{2}(sđ \overparen{EF} -sđ \overparen{PM})\) (góc có đỉnh bên ngoài đường tròn)
\(\Rightarrow sđ \overparen{EF}=2\widehat{N}+ sđ \overparen{PM}\)
+) \(\widehat{Q}=\dfrac{1}{2}(sđ \overparen{MF} -sđ \overparen{PE})\) (góc có đỉnh bên ngoài đường tròn)
\(\Rightarrow sđ \overparen{MF}=2 \widehat{Q}+sđ \overparen{PE}\)
\(\Rightarrow sđ \overparen{MF}+sđ\overparen{EF}\)\(=2 (\widehat{Q}+\widehat{N})+(sđ \overparen{PE}+sđ \overparen{PM})\)
\(\Rightarrow sđ \overparen{ME}(lớn)\)\(= 2 (\widehat{Q}+\widehat{N})+sđ \overparen{ME}(nhỏ)\)
Mà \(sđ \overparen{ME}(lớn)=360^\circ-sđ \overparen{ME}(nhỏ)\)
\(\Rightarrow 360^\circ-sđ \overparen{ME}(nhỏ)\)\(= 2 (\widehat{Q}+\widehat{N})+sđ \overparen{ME}(nhỏ)\)
\(\Rightarrow sđ \overparen{ME}(nhỏ) =180^\circ-(\widehat{Q}+\widehat{N})\)\(=180^\circ-(35^\circ+45^\circ)=100^\circ\)
Do đó: \(\widehat{MFE}= \dfrac{1}{2}sđ\overparen{ME}(nhỏ)\)\(= \dfrac{1}{2}.100^\circ=50^\circ\)
Vậy chọn \((A)\) \(50^\circ\)
-- Mod Toán 9 HỌC247
-


Bài 79 trang 114 sách bài tập toán 9 tập 2
bởi Tieu Dong
 08/10/2018
08/10/2018
Bài 79 (Sách bài tập - tập 2 - trang 114)
Cho nửa đường tròn đường kính AB. Gọi C là một điểm chạy trên nửa đường tròn đó. Trên AC lấy điểm D sao cho AD = CB. Qua A kẻ tiếp tuyến với nửa đường tròn rồi lấy AE = AB (E và C cùng thuộc một nửa mặt phẳng bờ AB)
a) Tìm quỹ tích điểm D
b) Tính diện tích phần chung của hai nửa đường tròn đường kính AB và AE
Theo dõi (0) 1 Trả lời -


Bài 78 trang 114 sách bài tập toán 9 tập 2
bởi Nguyễn Hạ Lan
 08/10/2018
08/10/2018
Bài 78 (Sách bài tập - tập 2 - trang 114)
Cho tam giác AHB có \(\widehat{H}=90^0,\widehat{A}=30^0,BH=4cm\). Tia phân giác của góc B cắt AH tại O. Vẽ đường tròn (O; OH) và đường tròn (O; OA)
a) Chứng minh đường tròn (O; OH) tiếp xúc với cạnh AB
b) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên
Theo dõi (0) 1 Trả lời -


Bài 77 trang 114 sách bài tập toán 9 tập 2
bởi Nguyễn Lê Thảo Trang
 08/10/2018
08/10/2018
Bài 77 (Sách bài tập - tập 2 - trang 114)
Tính diện tích của phần gạch sọc trên hình 15 (theo kích thước đã cho trên hình)
Theo dõi (0) 1 Trả lời -


Bài 76 trang 114 sách bài tập toán 9 tập 2
bởi Hoàng My
 08/10/2018
08/10/2018
Bài 76 (Sách bài tập - tập 2 - trang 114)
Hai ròng rọc có tâm O, O' và bán kính R = 4a, R'=a. Hai tiếp tuyến chung MN và PQ cắt nhau tại A theo góc \(60^0\) (h.14). Tìm độ dài của dây curoa mắc qua hai ròng rọc ?
Theo dõi (0) 1 Trả lời -


Bài 75 trang 114 sách bài tập toán 9 tập 2
bởi het roi
 08/10/2018
08/10/2018
Bài 75 (Sách bài tập - tập 2 - trang 114)
Cho tam giác ABC có ba góc nhọn. Dựng điểm M nằm trong tam giác ABC sao cho \(\widehat{AMB}=\widehat{BMC}=\widehat{CMA}\) ?
Theo dõi (0) 1 Trả lời -


Bài 74 trang 114 sách bài tập toán 9 tập 2
bởi Nguyễn Thủy Tiên
 08/10/2018
08/10/2018
Bài 74 (Sách bài tập - tập 2 - trang 114)
Cho lục giác đều ABCDEF. Chứng minh rằng đường chéo BF chia AD thành hai đoạn thẳng theo tỉ số 1 : 3 ?
Theo dõi (0) 1 Trả lời





