Bài tập 3.10 tr 116 sách BT Toán lớp 9 Tập 2
Tam giác đều \(ABC\) nội tiếp đường tròn tâm \(O\) bán kính \(R.\) Khi đó, \(\widehat {BOC}\) có số đo bằng bao nhiêu\(?\)
\((A)\) \( 60^\circ ; \) \((B)\) \( 120^\circ ; \)
\((C)\) \( 240^\circ ; \) \( (D)\) Không tính được.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải chi tiết
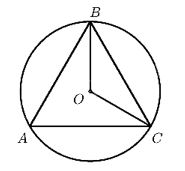
Xét đường tròn \((O),\) ta có: \(\widehat{BAC}=\dfrac{1}{2}\widehat{BOC}\) (số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung)
Nên \(\widehat{BOC}=2\widehat{BAC}=2.60^\circ=120^\circ\)
Vậy chọn \((B)\) \( 120^\circ \)
-- Mod Toán 9 HỌC247
-


Bài 73 trang 113 sách bài tập toán 9 tập 2
bởi thủy tiên
 08/10/2018
08/10/2018
Bài 73 (Sách bài tập - tập 2 - trang 113)
Cho đường tròn đường kính AB. Qua A và B kẻ hai tiếp tuyến của đường tròn đó. Gọi M là một điểm trên đường tròn. Các đường thẳng AM và BM cắt các tiếp tuyến trên lần lượt tại B' và A'
a) Chứng minh rằng \(AA'.BB'=AB^2\)
b) Chứng minh rằng \(A'A^2=A'M.A'B\)
Theo dõi (0) 1 Trả lời -


Chứng minh góc EDF =90 độ
bởi Mai Anh
 21/02/2019
21/02/2019
Cho tam giác ABC cố định vuông tại A , đường cao AD . Vẽ (O) ngoại tiếp tam giác ABD và (O') ngoại tiếp tam giác ACD . Qua A kẻ đường thẳng d bất kì không cắt đoạn BC . Gọi giap điểm của D với đường tròn (O) là E và (O') là F . Gọi M là giao điểm của DE với AB và N là giao điểm của DF với AC .
a, Chứng minh góc EDF =90 độ
b, chứng minh MN song song EF
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác MAOB nội tiếp đường tròn
bởi thi trang
 22/02/2019
22/02/2019
Cho điểm M nằm ngoài đường tròn (O) .Qua M vẽ các tiếp tuyến MA,MB ( A,B là các tiếp điểm ) và đường thẳng d không đi qua O cắt đường tròn (O) tại C,D ( C nằm giữa M và D). Đoạn thẳng OM cắt AB và (O) theo thứ tự tại H và I.chứng minh rằg: a)tứ giác MAOB nội tiếp đường tròn b) góc MAC = góc ADC từ đó suy ra MC.MD=MH.MO c)CI là tia phân giác của MCH
Theo dõi (0) 1 Trả lời -


Chứng minh MA.MB = ME . MF
bởi Nguyễn Thủy
 21/02/2019
21/02/2019
Cho đường tròn O và điểm M nằm ngoài đường tròn.Đường thẳng MO cắt (O) tại E và F(EM<FM).Vẽ cát tuyến MAB và tieeps tuyến MC của (O) ( C là tiếp điểm;A nằm giữa M và B ; A và C nằm khác phía đối vs đường thẳng MO.
1)CMR: MA.MB = ME . MF(câu này làm đc r nhé)
2) Gọi H là hình chiếu vuông góc của điểm C trên đường thẳng MO.CMR :AHOB là tứ giác nội tiếp.
(làm ơn trình bày câu này kĩ kĩ nhé,chứ méo hiểu j thì chết,t rất ngu)
3)TRên nửa mặt phẳng bờ là đường thẳng MO có chứa điểm A,vẽ nữa đương tròn đường kính MF.Nửa đường tròn này cắt tiếp tuyến tại E của ( O) tại K .Gọi S là giao điểm của hai đường thẳng CO và KC> CMR: đường thẳng MS vuông góc vs đường thẳng KC.
4)Gọi P,Q lần lượt là tâm đường tròn nghoại tiếp ccas tam gaics É<ABS< và T là trung điểm của KS .CMR : P , Q ,T thẳng hàng.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Vẽ đường cao AH, đường tròn tâm O đường kính AH cắt AB tại E và cắt AC tại điểm F.
a) Chứng minh tứ giác AEHF là hình chữ nhật
b) Chứng minh tứ giác BEFC nội tiếp
c) Gọi I là trung điểm của BC. Chứng minh AI vuông góc với EF
d) Gọi K là tâm của đường tròn ngoại tiếp tứ giác BEFC. Tính diện tích hình tròn tâm K.
Giải giúp mình với mai kiểm tra rồi
Theo dõi (0) 1 Trả lời -


Chứng minh AECD là tứ giác nội tiếp
bởi Nguyễn Thị Thúy
 22/02/2019
22/02/2019
từ một điểm M nằm ngoài đường tròn tâm O vẽ hai tia tiếp tuyến MA và MB với đường tròn. trên cung nhỏ AB lấy một điểm C. vẽ CD, CE lần lượt vuông góc với AB, MA. chứng minh: a, AECD là tứ giác nội tiếp , b, ABC=EDC
Theo dõi (0) 1 Trả lời





