Bài tập 76 trang 114 SBT Toán 9 Tập 2

31 BT SGK

Bài tập 76 tr 114 sách BT Toán lớp 9 Tập 2

Hai ròng rọc có tâm $O, O’$ và bán kính $R = 4a,$ $R’ = a.$ Hai tiếp tuyến chung $MN$ và $PQ$ cắt nhau tại $A$ theo góc $60^\circ.$ Tìm độ dài của dây cua- roa mắc qua hai ròng rọc.

Hình học 9 Chương 3 Bài 11 Trắc nghiệm Hình học 9 Chương 3 Bài 11 Giải bài tập Hình học 9 Chương 3 Bài 11

Hướng dẫn giải chi tiết

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với cotang góc kề.

+) Trong đường tròn $R,$ độ dài $l$ của một cung $n^\circ$ được tính theo công thức: $l=\dfrac{\pi Rn}{180}.$

Lời giải chi tiết

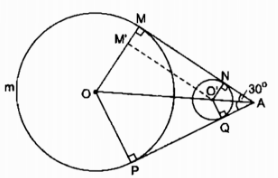
Vì hai tiếp tuyến chung của đường tròn (O) và (O’) cắt nhau tại A nên O, O’, A thẳng hàng.

$\widehat {OAM} = \widehat {OAP} = {1 \over 2}\widehat {MAP}$ (tính chất hai tiếp tuyến cắt nhau)

$ \Rightarrow \widehat {OAM} = {30^0}$

Trong tam giác vuông OMA có $\widehat {OMA} = {90^0}$

$ \Rightarrow MA = OM.\cot \widehat {OAM}$

$ = 4a\cos {30^0} = 4a\sqrt 3 $

Trong tam giác vuông O’NA có$\widehat {O'NA} = {90^0}$

$ \Rightarrow NA = O'N\cot \widehat {O'AN} = a\cot {30^0} = a\sqrt 3 $

$MN = MA - NA = 4a\sqrt 3 - a\sqrt 3 = 3a\sqrt 3 $

Trong tứ giác O’NAQ có $\widehat N = \widehat Q = {90^0}$; $\widehat A = {60^0}$

Suy ra: $\widehat {NO'Q} = {120^0}$

Độ dài cung nhỏ $\overparen{NQ}$ là: ${l_1} = {{\pi .a.120} \over {180}} = {{2\pi a} \over 3}$

Trong tứ giác OMAP có $\widehat M = \widehat P = {90^0}$; $\widehat A = {60^0}\$

Suy ra: $\widehat {MOP} = {120^0}$ nên số đo cung nhỏ $\overparen{MP}$ bằng 120⁰

sđ $\overparen{MnP}$ $ = {360^0} - {120^0} = {240^0}$

Độ dài cung lớn $\overparen{MnP}$ là ${l_2}$ $ = {{\pi .4a.240} \over {180}} = {{16\pi a} \over 3}$

Chiều dài của dây cua – roa mắc qua hai ròng rọc là:

\(2MN + {l_1} + {l_2} = 2.3a\sqrt 3 + {{2\pi a} \over 3} + {{16\pi a} \over 3}\(

=$6a\sqrt 3 + 6\pi a = 6a\left( {\sqrt 3 + \pi } \right)$

-- Mod Toán 9 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 76 trang 114 SBT Toán 9 Tập 2 HAY thì click chia sẻ

YOMEDIA

Chứng minh 3 điểm E,H,F cùng nằm trên một đường tròn biết M vuông góc với AC tại M

bởi Ly Tâm 30/03/2019

Cho tam giác ABC nhọn nội tiếp đường tròn (O;R), vẽ đường cao AK và đường kính AD. Vẽ BM vuông góc với AC tại M, AK và BM giao tại H, CH cắt AB tại N. BM kéo dài cắt (O) tại E và CN cắt (O) tại F.

Chứng minh 3 điểm E,H,F cùng nằm trên một đường tròn, xác định tâm đường tròn đó

Theo dõi (0) 0 Trả lời
Chứng minh tứ giác NKOM nội tiếp biết đường tròn tâm O đường kính BC cắt AB và AC

bởi Ly Tâm 15/03/2019

Cho tam giác ABC có 3 góc nhọn (AB<AC). Vẽ đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại N, M. Gọi H là giao điểm của BM vfa CN; AH cắt BC tại K.
a) Chứng minh tứ giác ANKC nội tiếp
b) Gọi I là giao điểm của NK và BM. Chứng minh: IH.NM=IN.MH
c) Chứng minh tứ giác NKOM nội tiếp

Theo dõi (0) 1 Trả lời
Chứng minmh MB^2=MK.MN biết cát tuyến MKN không qua O

bởi Ly Tâm 13/03/2019

Cho đường tròn (O:R). Từ M ở ngoài (O), kẻ hai tiếp tuyến MB và MC (B, C là 2 tiếp điểm)

a/ Cm tứ giác MBOC nội tiếp được đường tròn

b) Vẽ cát tuyến MKN không qua O. Cm: MB²=MK.MN

c) Trên (O) lấy A thuộc cung lớn BC sao cho AB song song KN. AC cắt KN tại I. Cm I là trung điểm KN

( câu a,b mình đã làm được rồi, chỉ mong các bạn giúp mình câu c)

Theo dõi (0) 0 Trả lời
Chứng minh KQ//EF biết tam giác ABC có 3 góc nhọn, các đường thẳng BE và CF

bởi Đào Thu Nguyệt 17/02/2019

Cho tam giác ABC có 3 góc nhọn các đường cao AD, BE, CF cắt nhau tại H. các đường thẳng BE và CF cắt (O) tại Q và K

1. Chứng minh 4 điểm B, E, F, C thuộc 1 đường tròn

2. Chứng minh KQ//EF

3. Gọi I là trung điểm BC, chứng minh tứ giác EFDI nội tiếp

4. Cho BC cố định, tìm vị trí điểm A để chu vi tam giác DEF max

Mọi người làm ơn giúp mình câu 3, 4 nhé!

Theo dõi (0) 1 Trả lời
Chứng minh AD.AE= AB^2 biết đường tròn (O;R) với dây BC cố định

bởi Đào Thu Nguyệt 15/02/2019

Cho đường tròn (O;R) với dây BC cố định (BC không đi qua O). Gọi A là điểm chính giữa cung nhỏ BC. Điểm E thuộc cung lớn BC. Nối AE cắt dây BC tại D. Gọi I là trung điểm dây BC. Hạ CH vuông góc với AE. đường thẳng BE cắt CH tại M
a) Chứng minh AHCI nội tiếp
b) Chứng minh AD.AE= AB^2
c) Cho BC = R $\sqrt{3}$ . Tính AC
d) Tìm vị trí điểm E để diện tích tam giác MAC max
giúp mình câu C thôi mn ơi

Theo dõi (0) 1 Trả lời
Xác định vị trí điểm M thuộc tia Ax sao cho góc BMC có số đo lớn nhất

bởi Đào Thu Nguyệt 12/02/2019

Cho góc nhọn xAy. Các điểm B, C thuộc tia Ay sao cho AB = a, AC= 4a (a>0). Xác định vị trí điểm M thuộc tia Ax sao cho góc BMC có số đo lớn nhất

Theo dõi (0) 0 Trả lời