Bài tập 74 tr 114 sách BT Toán lớp 9 Tập 2
Cho lục giác \(ABCDEF.\) Chứng minh rằng đường chéo \(BF\) chia \(AD\) thành hai đoạn thẳng theo tỉ số \(1: 3.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Số đo của nửa đường tròn bằng \(180^o.\)
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Trong hình thoi, hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết
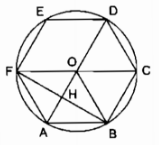
Lục giác đều ABCDEF nội tiếp trong đường tròn (O)
\(\overparen{AB}\) = \(\overparen{CB}\) = \(\overparen{CD}\) = \(\overparen{DE}\) = \(\overparen{EF}\) = \(\overparen{FA}\) = 600
\( \Rightarrow \) sđ \(\overparen{ABCD}\) = sđ \(\overparen{AB}\) + sđ \(\overparen{BC}\) + sđ \(\overparen{CD}\) = 1800
Nên AD là đường kính của đường tròn (O)
Ta có: OA = OB = OF = AB = AF = R
Nên tứ giác ABOF là hình thoi
Gọi giao điểm của AD và BF là H
Ta có: \(FB \bot OA\) (tính chất hình thoi)
\( \Rightarrow AH = HO = {{AO} \over 2} = {R \over 2}\)
\(HD = HO + OD = {R \over 2} + R = {{3R} \over 2}\)
Suy ra: \({{AH} \over {HD}} = {{{R \over 2}} \over {{{3R} \over 2}}} = {1 \over 3}\)
-- Mod Toán 9 HỌC247
-


Cho nửa đường tròn (O), đường kính AB=8cm, vẽ day AC tạo với AB một góc 30 độ. Vẽ tiếp tuyến Bx cắt đường thẳng AC tại D. Trên Bx lấy điểm E sao cho BE=BA. Chứng minh: AD=2BD
bởi Hương Giang
 09/03/2020
09/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Làm hộ mik
Làm hộ mik Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Cho tam giác nhọn ABC, trên nửa mặt phẳng bờ AC không chưa điểm B, lấy điểm D sao cho DA=DC và góc ACD=1/2góc ABC. Chứng minh rằng ABCD là tứ giác nội tiếp.
bởi Bảo Long
 24/02/2020
24/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho đường tròn (O;R), dây AB cố định (BC không đi qua O). Gọi A là điểm chính giữa cung nhỏ CB. Điểm N thuộc cung lớn BC, AN cắt BC tại D, kẻ CH vuông góc AN tại H, gọi AO ắt BC tại I, CH cắt O tại K, HI cắt KB tại Q. Chứng minh bốn điểm A, H, I, C thuộc ường tròn và tích AD.AN không đôỉ khi N di chuyển trên cung lớn BC.
bởi huyen pham ngoc
 21/02/2020
21/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Từ điểm M nằm ngoài đường tròn (O) vẽ 2 tiếp tuyến MP, MQ với đường tròn (P, Q là tiếp điểm), vẽ cát tuyến MAB, I là trung điểm AB. Chứng minh 5 điểm M, P, O, I, Q cùng thuộc một đường tròn.
bởi Hoàng Khánh Huyền
 16/02/2020
16/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Cho đường tròn (O) và một dây BC cố định không đi qua O. Trên tia đối của tia BC lấy một điểm A bất kì. Vẽ các tiếp tuyến AM, AN tới (O) (M, N là các tiếp điểm). MN cắt các đường AO và BC lần lượt ở H và K. Gọi I là trung điểm của BC.a) Vẽ dây MP song song BC. Chứng minh N, I, P thẳng hàngb) Khi A di động trên tia đối của tia BC, chứng minh trọng tâm tam giác MBC chạy trên một đường tròn cố định.Theo dõi (0) 0 Trả lời
Cho đường tròn (O) và một dây BC cố định không đi qua O. Trên tia đối của tia BC lấy một điểm A bất kì. Vẽ các tiếp tuyến AM, AN tới (O) (M, N là các tiếp điểm). MN cắt các đường AO và BC lần lượt ở H và K. Gọi I là trung điểm của BC.a) Vẽ dây MP song song BC. Chứng minh N, I, P thẳng hàngb) Khi A di động trên tia đối của tia BC, chứng minh trọng tâm tam giác MBC chạy trên một đường tròn cố định.Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 99 trang 105 SGK Toán 9 Tập 2
Bài tập 73 trang 113 SBT Toán 9 Tập 2
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 77 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





