Bài tập 92 tr 104 sách GK Toán lớp 9 Tập 2
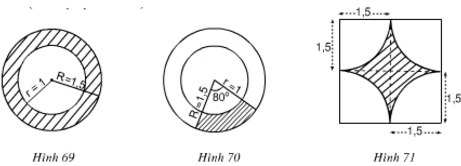
Hãy tính diện tích miền gạch sọc trong các hình 69, 70, 71 (đơn vị độ dài: cm).
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Công thức tính diện tích hình tròn bán kính R là: \(S = \pi {R^2}\)
+) Diện tích hình quạt tròn bán kính R, cung \({n^0}\) được tính theo công thức: \(S = \dfrac{{\pi {R^2}n}}{{360}}\left( {hay\,\,S = \dfrac{{lR}}{2}} \right)\)
Lời giải chi tiết
a) Hình 69
Diện tích hình tròn bán kính \(R= 1,5\) là: \({S_1} = πR^2 = π. 1,5^2 = 2,25π\)
Diện tích hình tròn bán kính \(r = 1\) là: \({S_2} = πr^2= π. 1^2 = π\)
Vậy diện tích miền gạch sọc là:
\(S = {S_1} – {S_2} = 2,25 π – π = 1,25 π\) (đvdt)
b) Hình 70
Diện tích hình quạt có bán kính \(R = 1,5\); \(n^0 = 80^0\)
\(\displaystyle {S_1} = {{\pi {R^2}n} \over {360}} = {{\pi 1,{5^2}.80} \over {360}} = {\pi \over 2}\)
Diện tích hình quạt có bán kính \(r = 1\); \(n^0 = 80^0\)
\(\displaystyle {S_2} = {{\pi {r^2}n} \over {360}} = {{\pi {{.1}^2}.80} \over {360}} = {{2\pi } \over 9}\)
Vậy diện tích miền gạch sọc là: \(\displaystyle S = {S_1} - {S_2} = {\pi \over 2} - {{2\pi } \over 9} = {{9\pi - 4\pi } \over {18}} = {{5\pi } \over {18}}\)
c) Hình 71
Diện tích hình vuông cạnh \(a = 3\) là:
\({S_1} = a^2 = 3^2 =9\)
Diện tích phần không gạch sọc bằng diện tích 4 quạt tròn bán kính \(R=1,5cm \) và có số đo cung là \(90^0\).
Hay tổng diện tích 4 quạt này bằng diện tích hình tròn bán kính \(R=1,5cm.\)
Diện tích hình tròn có \(R = 1,5\) là:
\({S_2} = πR^2 = π.1,5^2 = 2,25π = 7,06\)
Vậy diện tích miền gạch sọc là:
\(S = {S_1} – {S_2} = 9 – 7,06 = 1,94\) \((cm^2).\)
-- Mod Toán 9 HỌC247
-


Chứng minh OH vuông góc PQ?
bởi Võ Hoàng
 24/08/2020
24/08/2020
Cho tam giác đều ABC có đường cao AH, lấy điểm M tuỳ ý thuộc HC(M không trùng với H,C). Hình chiếu vuông góc của M lên AB, AC tại P,Q.
a, Chứng minh APMQ là tứ giác nội tiếp và xác định tâm O của đường tròn ngoại tiếp tứ giác APMQ;
b,CMR:BP.BA=BH.BM;
c. Chứng minh OH vuông góc PQ
Theo dõi (0) 3 Trả lời -


Rút gọn biểu thức \(A = \left( {\sqrt 6 - \sqrt 3 } \right).\sqrt 3 - 3\sqrt 2 \)?
bởi Tú Uyên
 12/08/2020
12/08/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh rằng tứ giác AEKF là tứ giác nội tiếp?
bởi Nguyễn Hà Dương
 09/08/2020
09/08/2020
Cho tam giác nhọn ABC ( AB >AC ) đường tròn đường kính BC cắt AC và AB lần lượt tại E và F , gọi K là giao điểm của BF và CE
1) chứng minh rằng tứ giác AEKF là tứ giác nội tiếp
2) chứng minh rằng hai tam giác AFE và ABC đồng dạng
3) trong tam giác FBC kẻ đường cao FH , giả sử cho FH =4 cm , BH =8cm. Tính độ dài BCTheo dõi (1) 1 Trả lời -


Chứng minh tứ giác AKNH nội tiếp?
bởi Lê Ngọc Ánh
 31/07/2020
31/07/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh tứ giác AMDE nội tiếp?
bởi Trịnh Minh Thư
 26/07/2020
26/07/2020
Cho nửa đường tròn tâm O , đường kính AB =2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M nằm trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn ( C là tiếp điểm ) . AC cắt OM tại E , MB cắt nửa đường tròn tại D
a) Chứng minh AMDE là tgnt
b) Góc ADE = góc ACO
c) Tia BC cắt Ax tại N. Chứng minh M là trung điểm của AN
d) Vẽ CH vuông góc với AB ( H thuộc AB). Gọi I là trung điểm của CH. Cmr 3 điểm M , I , B thẳng hàng
Theo dõi (0) 0 Trả lời -


Chứng minh C, M, D thẳng hàng?
bởi Trần anh tuấn Tuấn
 22/07/2020
22/07/2020
Cho đường tròn tâm O đường kính AB. Cho M là điểm bất kì trên đường tròn, kẻ MH buông góc với AB tại H,vẽ đường tròn tâm M bán kính MH kẻ các tiếp tuyến AC,BD với đường tròn M, C và D là các tiếp điểm
a) Chứng minh C,M,D thẳng hàng
b) Chứng minh CD là tiếp tuyến của đường tròn tâm O.
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 90 trang 104 SGK Toán 9 Tập 2
Bài tập 91 trang 104 SGK Toán 9 Tập 2
Bài tập 93 trang 104 SGK Toán 9 Tập 2
Bài tập 94 trang 105 SGK Toán 9 Tập 2
Bài tập 95 trang 105 SGK Toán 9 Tập 2
Bài tập 96 trang 105 SGK Toán 9 Tập 2
Bài tập 97 trang 105 SGK Toán 9 Tập 2
Bài tập 98 trang 105 SGK Toán 9 Tập 2
Bài tập 99 trang 105 SGK Toán 9 Tập 2
Bài tập 73 trang 113 SBT Toán 9 Tập 2
Bài tập 74 trang 114 SBT Toán 9 Tập 2
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 77 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





