Giải bài tập SGK Chương 4 Hình học 9 Tập 2

Hãy nêu tên mỗi góc trong các hình dưới đây:

(Ví dụ. góc trên hình 66b) là góc nội tiếp).

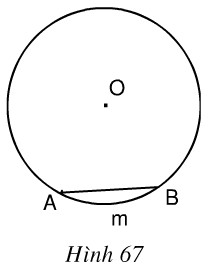
Trong hình 67, cung $AmB$ có số đo là $66^0$. Hãy:

a) Vẽ góc ở tâm chắn cung $AmB$. Tính góc $AOB$.

b) Vẽ góc nội tiếp đỉnh $C$ chắn cung $AmB$. Tính góc $ACB$.

c) Vẽ góc tạo bởi tia tiếp tuyến $Bt$ và dây cung $BA$. Tính góc $ABt$.

d) Vẽ góc $ADB$ có đỉnh $D$ ở bên trong đường tròn. So sánh $\widehat {A{\rm{D}}B}$  với $\widehat {ACB}$ .

e) Vẽ góc $AEB$ có đỉnh $E$ ở bên ngoài đường tròn ($E$ và $C$ cùng phía đối với $AB$). So sánh $\widehat {A{\rm{E}}B}$ với $\widehat {ACB}$

a) Vẽ hình vuông cạnh $4cm$.

b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính $R$ của đường tròn này.

c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính $r$ của đường tròn này. 

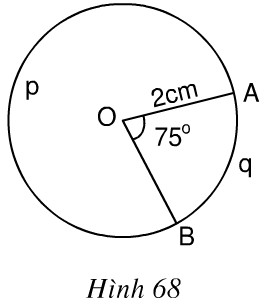
Trong hình 68, đường tròn tâm O có bán kính $R = 2cm$, góc $AOB = 75^0$.

a) Tính số đo cung $ApB$.

b) Tính độ dài hai cung $AqB$ và $ApB$.

c) Tính diện tích hình quạt tròn $OAqB$ 

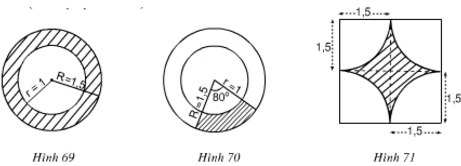
Hãy tính diện tích miền gạch sọc trong các hình 69, 70, 71 (đơn vị độ dài: cm).

Có ba bánh xe răng cưa $A, B, C$ cùng chuyển động ăn khớp với nhau. Khi một bánh xe quay thì hai bánh xe còn lại cũng quay theo. Bánh xe $A$ có $60$ răng, bánh xe B có $40$ răng, bánh xe $C$ có $20$ răng. Biết bán kính bánh xe $C$ là $1$cm. Hỏi:

a) Khi bánh xe $C$ quay $60$ vòng thì bánh xe $B$ quay mấy vòng?

b) Khi bánh xe $A$ quay $80$ vòng thì bánh xe $B$ quay mấy vòng?

c) Bán kính của các bánh xe $A$ và $B$ là bao nhiêu?  

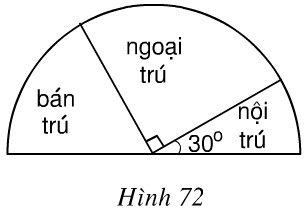
Hãy xem biểu đồ hình quạt biểu diễn sự phân phối học sinh của một trường THCS theo diện ngoại trú, bán trú, nội trú (h.72). Hãy trả lời các câu hỏi sau:

a) Có phải $\displaystyle {1 \over 2}$ số học sinh là học sinh ngoại trú không?

b) Có phải $\displaystyle {1 \over 3}$ số học sinh là học sinh bán trú không?

c) Số học sinh nội trú chiếm bao nhiêu phần trăm?

d) Tính số học sinh mỗi loại, biết tổng số học sinh là $1800$ em. 

Các đường cao hạ từ $A$ và $B$ của tam giác $ABC$ cắt nhau tại $H$ (góc $C$ khác $90^0$) và cắt đường tròn ngoại tiếp tam giác $ABC$ lần lượt tại $D$ và $E$. Chứng minh rằng:

a) $CD = CE$ ;    

b) $ΔBHD$ cân ;    

c) $CD = CH$. 

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và tia phân giác của góc $A$ cắt đường tròn tại $M$. Vẽ đường cao $AH$. Chứng minh rằng:

a) $OM$ đi qua trung điểm của dây $BC$.

b) $AM$ là tia phân giác của góc $OAH$.

Cho tam giác $ABC$ vuông ở $A$. Trên $AC$ lấy một điểm $M$ và vẽ đường tròn đường kính $MC$. Kẻ $BM$ cắt đường tròn tại $D$. Đường thẳng $DA$ cắt đường tròn tại $S$. Chứng minh rằng:

a) $ABCD$ là một tứ giác nội tiếp;

b) $\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}$ ;

c) $CA$ là tia phân giác của góc $SCB$ 

Cho đường tròn $(O)$ và một điểm $A$ cố định trên đường tròn. Tìm quỹ tích các trung điểm $M$ của dây $AB$ khi điểm $B$ di động trên đường tròn đó.

 Dựng $ΔABC$, biết $BC = 6cm$, góc $\widehat{BAC} = 80^0$, đường cao $AH$ có độ dài là $2cm$. 

Cho đường tròn đường kính $AB.$ Qua $A$ và $B$ kẻ hai tiếp tuyến của đường tròn đó. Gọi $M$ là một điểm trên đường tròn. Các đường thẳng $AM$ và $BM$ cắt các tiếp tuyến trên lần lượt tại $B’$ và $A’.$

$a)$ Chứng minh rằng ${\rm{AA}}'.BB' = A{B^2}$

$b)$ Chứng minh rằng $A'{A^2} = A'M.A'B$

Cho lục giác $ABCDEF.$ Chứng minh rằng đường chéo $BF$ chia $AD$ thành hai đoạn thẳng theo tỉ số $1: 3.$

Cho tam giác $ABC$ có ba góc nhọn. Dựng điểm $M$ nằm trong tam giác $ABC$ sao cho $\widehat {AMB} = \widehat {BMC} = \widehat {CMA}$

Hai ròng rọc có tâm $O, O’$ và bán kính $R = 4a,$ $R’ = a.$ Hai tiếp tuyến chung $MN$ và $PQ$ cắt nhau tại $A$ theo góc $60^\circ.$ Tìm độ dài của dây cua- roa mắc qua hai ròng rọc.

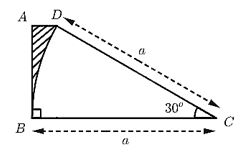
Tính diện tích phần gạch sọc trên hình sau (theo kích thước đã cho trên hình)

Cho tam giác $AHB$ có $\widehat H = 90^\circ ,\widehat A = 30^\circ$ và $BH = 4cm.$ Tia phân giác của góc $B$ cắt $AH$ tại $O.$ Vẽ đường tròn $(O; OH)$ và đường tròn $(O; OA).$

$a)$ Chứng minh đường tròn $(O; OH)$ tiếp xúc với cạnh $AB.$

$b)$ Tính diện tích hình vành khăn nằm giữa hai đường tròn trên.

Cho nửa đường tròn đường kính $AB.$ Gọi $C$ là một điểm chạy trên nửa đường tròn đó. Trên $AC$ lấy điểm $D$ sao cho $AD = CB.$ Qua $A$ kẻ tiếp tuyến với nửa đường tròn rồi lấy $AE = AB$ ($E$ và $C$ cùng thuộc một nửa mặt phẳng bờ $AB$)

$a)$ Tìm quỹ tích điểm $D$

$b)$ Tính diện tích phần chung của hai nửa hình tròn đường kính $AB$ và $AE.$

Cho tam giác đều $ACB$ và $ACD,$ cạnh $a.$ Lần lượt lấy $B$ và $D$ làm tâm vẽ hai đường tròn bán kính $a.$ Kẻ các đường kính $ABE$ và $ADF.$ Trên cung nhỏ $CE$ của đường tròn tâm $B$ lấy điểm $M$ (không trùng với $E$ và $C$). Đường thẳng $CM$ cắt đường tròn tâm $D$ tại điểm thứ hai là $N.$ Hai đường thẳng $EM$ và $NF$ cắt nhau tại điểm $T.$ Gọi $H$ là giao điểm của $AT$ và $MN.$ Chứng minh:

$a)$ $MNT$ là tam giác đều.

$b)$ $AT = 4AH.$

Cho đường tròn tâm $O$ bán kính $R$ và điểm $M$ ở ngoài đường tròn đó. Qua điểm $M$ kẻ hai tiếp tuyến $MA,$ $MB$ và cát tuyến $MCD$ với đường tròn $(O),$ trong đó điểm $C$ ở giữa hai điểm $M, D.$ Đường thẳng qua điểm $C$ và vuông góc với $OA$ cắt $AB$ tại $H.$ Gọi $I$ là trung điểm của dây $CD.$ Chứng minh $HI$ song song với $AD.$

Góc nội tiếp là góc:

$(A)$ có đỉnh nằm trên đường tròn.

$(B)$ có hai cạnh là hai dây của đường tròn.

$(C)$ có hai đỉnh là tâm đường tròn và có hai cạnh là hai bán kính.

$(D)$ có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.

Một đường tròn là đường tròn nội tiếp nếu nó:

$(A)$ đi qua các đỉnh của một tam giác.

$(B)$ tiếp xúc với các đường thẳng chứa các cạnh của một tam giác.

$(C)$ tiếp xúc với các cạnh của một tam giác.

$(D)$ nằm trong một tam giác.

Một tứ giác là tứ giác nội tiếp nếu

$(A)$ có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau.

$(B)$ có $4$ góc bằng nhau.

$(C)$ có $4$ cạnh bằng nhau.

$(D)$ có các cạnh tiếp xúc với đường tròn.

Quỹ tích các điểm $M$ nhìn đoạn thẳng $AB$ dưới một góc $120^\circ$ là

$(A)$ một đường tròn đi qua hai điểm $A, B.$

$(B)$ một đường thẳng song song với $AB.$

$(C)$ một cung chứa góc $120^\circ$ dựng trên hai điểm $A, B.$

$(D)$ hai cung chứa góc $120^\circ$ (đối xứng nhau) dựng trên hai điểm $A, B.$

Độ dài của nửa đường tròn có đường kính $8R$ bằng:

$(A)$ $πR;$                     $(B)$ $2πR;$

$(C)$ $4πR;$                   $(D)$ $8πR.$

Diện tích của nửa hình tròn có đường kính $4R$ bằng:

$(A)$$\dfrac{1}{2}\pi R^2;$                 

$(B)$ $\pi R^2;$   

$(C)$ $2\pi R^2;$                     

$(D)$ $4\pi R^2;$ 

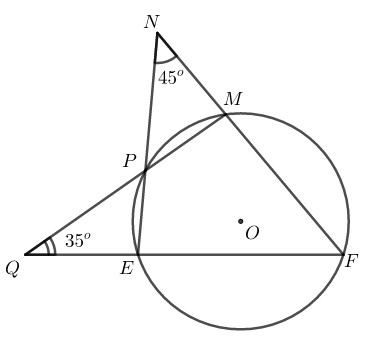
Cho hình sau. Khi đó, số đo của $\widehat {MFE}$ bằng bao nhiêu$?$

$(A)$ $50^\circ;$               $(B)$ $80^\circ;$

$(C)$ $130^\circ;$             $(D)$ Không tính được.

Tam giác đều $ABC$ nội tiếp đường tròn tâm $O$ bán kính $R.$ Khi đó, $\widehat {BOC}$ có số đo bằng bao nhiêu$?$

$(A)$ $60^\circ ;$                $(B)$ $120^\circ ;$  

$(C)$ $240^\circ ;$              $(D)$ Không tính được.

Hình vuông $XYZT$ nội tiếp đường tròn tâm $O$ bán kính $R.$ điểm $M$ bất kì thuộc cung nhỏ $XT,$ $\widehat {ZMT}$ có số đo bằng bao nhiêu$?$

$(A)$ $23^\circ30';$       

$(B)$ $45^\circ;$

$(C)$ $90^\circ;$             

$(D)$ Không tính được. 

Cho hình như hình bên $(PQ = PR;$ $QY$ và $RX$ là các tia phân giác$).$ Khi đó, $PYKX$ là:

$(A)$ hình thang và không phải là hình bình hành.

$(B)$  hình bình hành và không phải hình thoi.

$(C)$  hình thoi và không phải hình chữ nhật.

$(D)$ hình chữ nhật.