Bài tập 97 tr 105 sách GK Toán lớp 9 Tập 2
Cho tam giác \(ABC\) vuông ở \(A\). Trên \(AC\) lấy một điểm \(M\) và vẽ đường tròn đường kính \(MC\). Kẻ \(BM\) cắt đường tròn tại \(D\). Đường thẳng \(DA\) cắt đường tròn tại \(S\). Chứng minh rằng:
a) \(ABCD\) là một tứ giác nội tiếp;
b) \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}\) ;
c) \(CA\) là tia phân giác của góc \(SCB\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+ Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: Nếu hai đỉnh kề một cạnh của một tứ giác cùng nhìn cạnh đối diện dưới các góc bằng nhau thì tứ giác đó là tứ giác nội tiếp.
+ Sử dụng: “Hai góc nội tiếp cùng chắn một cung thì bằng nhau”
Lời giải chi tiết
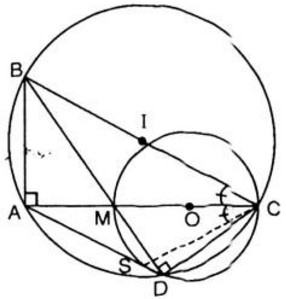
a) Ta có góc \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn \((O)\) nên \(\widehat {MDC} = {90^0}\)
⇒ \(∆CDB\) là tam giác vuông nên nội tiếp đường tròn đường kính \(BC\) .
Ta có \(∆ABC\) vuông tại \(A\).
Do đó \(∆ABC\) nội tiếp trong đường tròn tâm \(I\) đường kính \(BC\).
Ta có \(A\) và \(D\) cùng nhìn \(BC\) dưới một góc \(90^0\) không đổi nên tứ giác \(ABCD\) nội tiếp đường tròn đường kính \(BC\)
b) Ta có \(\widehat {AB{\rm{D}}}\) là góc nội tiếp trong đường tròn \((I)\) chắn cung \(AD\).
Tương tự góc \(\widehat {AC{\rm{D}}}\) là góc nội tiếp trong đường tròn \((I)\) chắn cung \(AD\)
Vậy \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}\)
c) Ta có:
\(\widehat {S{\rm{D}}M} = \widehat {SCM}\) (vì góc nội tiếp cùng chắn cung \(MS\) của đường tròn \((O)\))
\(\widehat {A{\rm{D}}B} = \widehat {ACB}\) (là góc nội tiếp cùng chắn cung \(AB\) của đường tròn \((I)\)
Mà \(\widehat {A{\rm{D}}B} = \widehat {S{\rm{D}}M} \Rightarrow \widehat {SCM} = \widehat {ACB}\)
Vậy tia \(CA\) là tia phân giác của góc \(SCB\)
-- Mod Toán 9 HỌC247
-


Cho nửa đường tròn (O;R), đường kính AB cố định. Qua A, B vẽ các tiếp tuyến với nửa đường tròn. Từ 1 điểm M tùy ý trên nửa đường tròn vẽ tiếp tuyến thứ 3 với nửa đường tròn cắt các tiếp tuyến tại A, B theo thứ tự là H, K
bởi Nguyễn Bảo Chi
 22/05/2020
22/05/2020
a) chứng minh tứ giác AHMO là tứ giác nội tiếp
b) chứng minh AH BK = HK
c) chứng minh ∆HAO đồng dạng với ∆AMB và HO. MB = 2R^2
Theo dõi (0) 0 Trả lời -

 Cho hai đường tròn O và O phẩy tiếp xúc ngoài nhau tại A Vẽ một tắt tiếng của A cắt đường tròn O tại B và C Chứng minh rằng các tiếp tuyến B và C sing song vs nhauTheo dõi (0) 1 Trả lời
Cho hai đường tròn O và O phẩy tiếp xúc ngoài nhau tại A Vẽ một tắt tiếng của A cắt đường tròn O tại B và C Chứng minh rằng các tiếp tuyến B và C sing song vs nhauTheo dõi (0) 1 Trả lời -


Tính góc AOB?
bởi Đỗ Thu Hiền
 10/05/2020
Giải hộ mình nha
10/05/2020
Giải hộ mình nha Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Cho tam giác ABC nội tiếp đường tròn tâm O.Dây cung AD vuông góc BC.Gọi E đối xứng D qua BC. Chứng minh E là trực tâm tam giác ABC.
bởi Tạ Khánh Băng
 07/05/2020
Bài 16 ấy ạ
07/05/2020
Bài 16 ấy ạ Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh rằng khi M di chuyển trên ABthì È luôn tiếp xúc với một đường tròn cố định?
bởi Lưu Thành Đạt
 05/05/2020
Chủ yếu ý 4. Cảm ơn nhiều
05/05/2020
Chủ yếu ý 4. Cảm ơn nhiều Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh rằng tứ giác AEMO nội tiếp?
bởi Nguyễn Thị Huyền Trang
 03/05/2020
03/05/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 95 trang 105 SGK Toán 9 Tập 2
Bài tập 96 trang 105 SGK Toán 9 Tập 2
Bài tập 98 trang 105 SGK Toán 9 Tập 2
Bài tập 99 trang 105 SGK Toán 9 Tập 2
Bài tập 73 trang 113 SBT Toán 9 Tập 2
Bài tập 74 trang 114 SBT Toán 9 Tập 2
Bài tập 75 trang 114 SBT Toán 9 Tập 2
Bài tập 76 trang 114 SBT Toán 9 Tập 2
Bài tập 77 trang 114 SBT Toán 9 Tập 2
Bài tập 78 trang 114 SBT Toán 9 Tập 2
Bài tập 79 trang 114 SBT Toán 9 Tập 2
Bài tập 3.1 trang 114 SBT Toán 9 Tập 2
Bài tập 3.2 trang 115 SBT Toán 9 Tập 2
Bài tập 3.3 trang 115 SBT Toán 9 Tập 2
Bài tập 3.4 trang 115 SBT Toán 9 Tập 2
Bài tập 3.5 trang 115 SBT Toán 9 Tập 2
Bài tập 3.6 trang 115 SBT Toán 9 Tập 2
Bài tập 3.7 trang 116 SBT Toán 9 Tập 2
Bài tập 3.8 trang 116 SBT Toán 9 Tập 2
Bài tập 3.9 trang 116 SBT Toán 9 Tập 2
Bài tập 3.10 trang 116 SBT Toán 9 Tập 2





