Giải bài 49 tr 127 sách GK Toán lớp 7 Tập 1
a) Tình các góc ở đáy của một tam giác cân biết góc ở đỉnh là 400
b) Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng 400
Hướng dẫn giải chi tiết
Câu a:
Gọi ABC là tam giác cân đã cho và góc ở định =400
Ta có +2
=1800
2= 1800 -
= 1400
=> = 700
Câu b:
Ta có: +
+
=1800
mà =
=400
nên +2
=1800
+800 =1800
=1000
-- Mod Toán 7 HỌC247
-

 Cho tam giác ABC cân tại B có góc B bằng 50 độ . Tính góc A và góc C
Cho tam giác ABC cân tại B có góc B bằng 50 độ . Tính góc A và góc C Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC, góc A=60 độ. Đường phân giác BD của góc B và phân giác CE của góc C cắt nhau tại I (D thuộc AC, E thuộc AB). Chứng minh: tam giác DEI cân.
bởi Đặng Hoàng Ngân Linh
 17/02/2020
Giúp vs
17/02/2020
Giúp vs Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -

 Cho tam giác ABC cân tại A có A = 50°a.Tính B,Cb.Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho . Chứng minh rằng: DE//BCTheo dõi (1) 5 Trả lời
Cho tam giác ABC cân tại A có A = 50°a.Tính B,Cb.Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho . Chứng minh rằng: DE//BCTheo dõi (1) 5 Trả lời -


Cho tam giác AOB cân tại O. Kể tia phân giác của góc AOB cắt AB tại H. Chứng minh HA=HB
bởi Đỗ Hà
 16/02/2020
Cho tam giác AOB cân tại O. Kể tia phân giác của góc AOB cắt AB tại H. a) chứng minh HA=HB? b) Trên cạnh OA lấy điểm M và trên cạnh OB lấy điểm N sao cho OM=ON. Chứng minh tam giác HMN cân ? c) Chứng minh MN//AB? d) Biết OB,OH lần lượt tỉ lệ với 5,4 và BA=6cm. Tính độ dài OH,OB,OA?Theo dõi (0) 0 Trả lời
16/02/2020
Cho tam giác AOB cân tại O. Kể tia phân giác của góc AOB cắt AB tại H. a) chứng minh HA=HB? b) Trên cạnh OA lấy điểm M và trên cạnh OB lấy điểm N sao cho OM=ON. Chứng minh tam giác HMN cân ? c) Chứng minh MN//AB? d) Biết OB,OH lần lượt tỉ lệ với 5,4 và BA=6cm. Tính độ dài OH,OB,OA?Theo dõi (0) 0 Trả lời -

 Ai giúp tôi với
Ai giúp tôi với Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác BAC có AB=AC=5cm, BC=8cm. Kẻ AH vuông góc với BC (H thuộc BC). Chứng minh HB=HC và góc BAH=góc CAH.
bởi Han Pham
 15/02/2020
15/02/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Cho tam giác ABC cân tại A, trên tia đối của tia CA lấy điểm D sao cho CD=CA. Kẻ AH vuông góc BC tại H. Kẻ DK vuông góc BC tại K. Chứng minh: ∆AHC=∆DKC
bởi Khánh Linh
 14/02/2020
14/02/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho ∆ ABC cân tại B.Trên cạnh BA và BC lần lượt lấy điểm E và D sao cho BD= BE. Chứng minh AE= CD, Gọi K là giao điểm của AE và CD. CM : KA= KC Chứng minh : BK đi qua trung điểm của AC
bởi Hakuenkun_ Hakuenku_
 13/02/2020
13/02/2020
Cho ∆ ABc cân tại B.Trên cạnh BA và BC lần lượt lấy điểm E và D sao cho BD= BE. Chứng minh AE= CD, Gọi K là giao điểm của AE và CD. CM : KA= KC
Chứng minh : BK đi qua trung điểm của AC
Theo dõi (0) 0 Trả lời -


Tính số đo của góc OAB và OBA
bởi Nguyễn Thị Thanh Mai
 13/02/2020
13/02/2020
Vẽ góc xOy =50 độ và tia phân giác ot.Lấy A thuộc Ox và B thuộc Oy sao cho OA=OB
1) Tính số đo của góc OAB và OBA
2)Ot cắt AB ở D.Chứng minh D là trung điểm của đoạn thẳng AB
Theo dõi (0) 0 Trả lời -


Chứng minh Bx//AC biết tam giác ABC cân tại B
bởi Ha My Vu
 11/02/2020
Cho tam giác ABC cân tại B. Gọi Bx là tia phân giác của góc ngoài tại đỉnh B . Chứng minh Bx//ACTheo dõi (2) 5 Trả lời
11/02/2020
Cho tam giác ABC cân tại B. Gọi Bx là tia phân giác của góc ngoài tại đỉnh B . Chứng minh Bx//ACTheo dõi (2) 5 Trả lời -

 Cho tam giác ABC cân tại A tính số đo các góc còn lại nếu biết a) A=40 độ b)B=50 độ c)C= 60 độTheo dõi (0) 0 Trả lời
Cho tam giác ABC cân tại A tính số đo các góc còn lại nếu biết a) A=40 độ b)B=50 độ c)C= 60 độTheo dõi (0) 0 Trả lời -

 Bài kiểm tra chất lượng
Bài kiểm tra chất lượng Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -

 Tam giác ABC cân tại A góc A = 80 độ Trên tia bc lấy E sao cho góc Bac = 50 độ trên AC lấy K sao cho a b k bằng 30 độ Trên cùng một nửa mặt phẳng bờ AB chứa C vẽ tam giác ABM đều A Chứng minh AE vuông góc với AB b, Ai giao với BK bằng h Chứng minh tam giác hik cân.Theo dõi (2) 1 Trả lời
Tam giác ABC cân tại A góc A = 80 độ Trên tia bc lấy E sao cho góc Bac = 50 độ trên AC lấy K sao cho a b k bằng 30 độ Trên cùng một nửa mặt phẳng bờ AB chứa C vẽ tam giác ABM đều A Chứng minh AE vuông góc với AB b, Ai giao với BK bằng h Chứng minh tam giác hik cân.Theo dõi (2) 1 Trả lời -


Cho tam giác ABC cân tại A, góc A bằng 2 lần góc B. Tính các góc của tam giác ABC.
bởi Nguyễn Hoàng Bảo Mun'z
 08/02/2020
08/02/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Cho ∆ABC vuông cân tại A, M là trung điểm của BC. Lấy điểm D bất kì thuộc cạnh BC. H và I theo thứ tự là hình chiếu của B và C xuống đường thẳng AD, đường thẳng AM cắt CI tại N. Chứng minh rằng: BH = AI.
bởi 罗舞
 06/02/2020
06/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác MNP can tại M. Trên cạnh MN lấy điểm I, trên cạnh MP lấy điểm K sao cho NI=PK. Chứng minh: ∆NIP=∆PKN
bởi Hoa Bỉ Ngạn
 02/02/2020
02/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC có BA = BC =5cm , AC =8 cm. Tia phân giác của góc B cắt AC tại D. Chứng minh rằng : tam giác BAD= tam giác BCD và BD vuông góc vs AC.
bởi Nguyễn Thành
 23/01/2020
23/01/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh tam giác ABM = tam giác ACM biết tam giác ABC cân tại A , M là trung điểm của BC
bởi Arora Quin
 22/01/2020
22/01/2020
Cho tam giác ABC cân tại A , M là trung điểm của BC . a) c/m tam giác ABM = tam giác ACM . Và AM vuông góc BC . b) Kẻ MK vuông góc AB ( K thuộc AB )MH vuông góc AC ( H thuộc AC ) cm BK=CH và tam giác MKH cân . c) cm KH//BC d) gọi O là giao điểm CK và BH , cm A,O,M thẳng hàng
Theo dõi (0) 4 Trả lời -


Chứng minh góc BDE= 90 độ biết tam giác ABC cân tại A đường phân giác BD
bởi Trần Văn Tài Anh
 22/01/2020
22/01/2020
cho tam giác ABC cân tại A đường phân giác BD. Trên tia BA lấy E sao cho BE =2CD. CMR góc BDE= 90 độ
Theo dõi (0) 2 Trả lời -


Tam giác CAB là tam giác gì biết góc xOy = 60°?
bởi Hú Le Pii Nè
 20/01/2020
20/01/2020
Cho góc xOy = 60°
A€Ox , B€ Oy , OA=OB
a) Tam giác CAB là tam giác gì?
b)M là trung điểm AB
CMR: OM vuông góc AB
c) từ A kẻ đường thẳng vuông góc với Ox
từ B kẻ đường thẳng vuông góc với Oy
2 đường thẳng cắt tại NO
CMR: BN= AN
d) Tính các góc của tam giác NAK
(K là giao điểm BN và Ox)
Theo dõi (0) 4 Trả lời -

 Giúp mk vớiTheo dõi (0) 1 Trả lời
Giúp mk vớiTheo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A (AB > AC). Tia phân giác góc A cắt BC tại D. Qua D kẻ đường thẳng vuông góc BC, cắt AC tại E. Trên AB lấy F sao cho AF = AE. Chứng minh rằng: góc B = góc DEC.
bởi Hốt Tặc Na Hạp
 14/01/2020
Cho tam giác ABC vuông tại A (AB > AC). Tia phân giác góc A cắt BC tại D. Qua D kẻ đường thẳng vuông góc BC, cắt AC tại E. Trên AB lấy F sao cho AF = AE. Chứng minh rằng: a, góc B = góc DEC. b, tam DBF là tam giác cân. c, DB = DETheo dõi (1) 0 Trả lời
14/01/2020
Cho tam giác ABC vuông tại A (AB > AC). Tia phân giác góc A cắt BC tại D. Qua D kẻ đường thẳng vuông góc BC, cắt AC tại E. Trên AB lấy F sao cho AF = AE. Chứng minh rằng: a, góc B = góc DEC. b, tam DBF là tam giác cân. c, DB = DETheo dõi (1) 0 Trả lời -


Cho tam giác ABC cân tại A, M là trung điểm của BC.Từ M kẻ MD song song với AC, ME song song với AB. Chứng minh rằng: tam giác BDM cân; ME=EC; AM vuông góc với DE.
bởi Tạ Thương
 03/01/2020
Giúp tôi vớiTheo dõi (0) 9 Trả lời
03/01/2020
Giúp tôi vớiTheo dõi (0) 9 Trả lời -


Tìm GTNN của biểu thức A=|x+2018|+|x+2019|
bởi Nhữ Thị Bích
 23/12/2019
Giúp tui với . Thanks
23/12/2019
Giúp tui với . Thanks Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Chứng minh tam giác OBC cân biết trên cạnh AB, AC lần lượt lấy điểm M, N sao cho AM=AN
bởi Tangk
 22/12/2019
22/12/2019
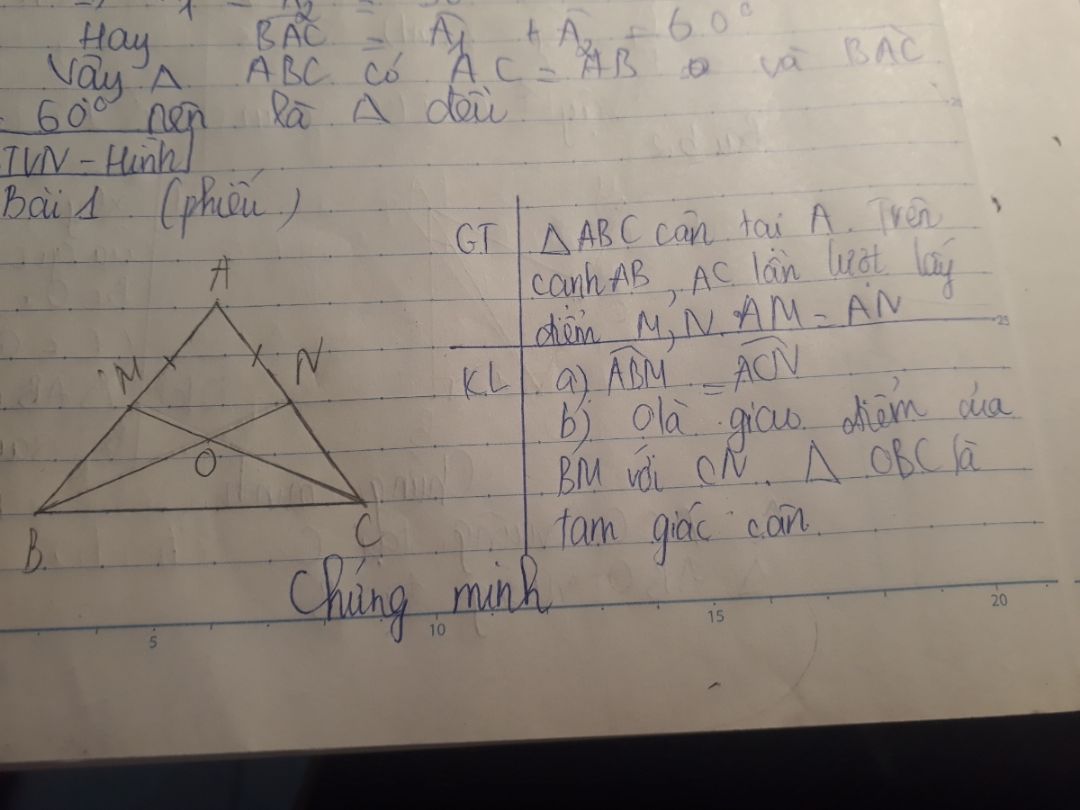 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Cho tam giác ABC cân tại A. Kẻ AM là tia phân giác của góc A. Trên tia đối tia MA lấy điểm E sao cho MA = ME. Chứng minh rằng: a) Tam giác ABM=tam giác ACM b) AM vuông góc với BC c) Góc BAM = góc CEM
Cho tam giác ABC cân tại A. Kẻ AM là tia phân giác của góc A. Trên tia đối tia MA lấy điểm E sao cho MA = ME. Chứng minh rằng: a) Tam giác ABM=tam giác ACM b) AM vuông góc với BC c) Góc BAM = góc CEM Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Cách chứng minh 3 điểm thẳng hàng
bởi vy Halen
 05/12/2019
Các bạn nào chỉ mình CÁC CÁCH CHỨNG MINH BA ĐIỂM THẲNG HÀNG đi. Mình cảm ơn trước!!!Theo dõi (0) 13 Trả lời
05/12/2019
Các bạn nào chỉ mình CÁC CÁCH CHỨNG MINH BA ĐIỂM THẲNG HÀNG đi. Mình cảm ơn trước!!!Theo dõi (0) 13 Trả lời -


Chứng minh M là trung điểm
bởi Hoàn Kim
 11/11/2019
Chỉ mình đi ạ mk đã vẽ sẵn hết r á
11/11/2019
Chỉ mình đi ạ mk đã vẽ sẵn hết r á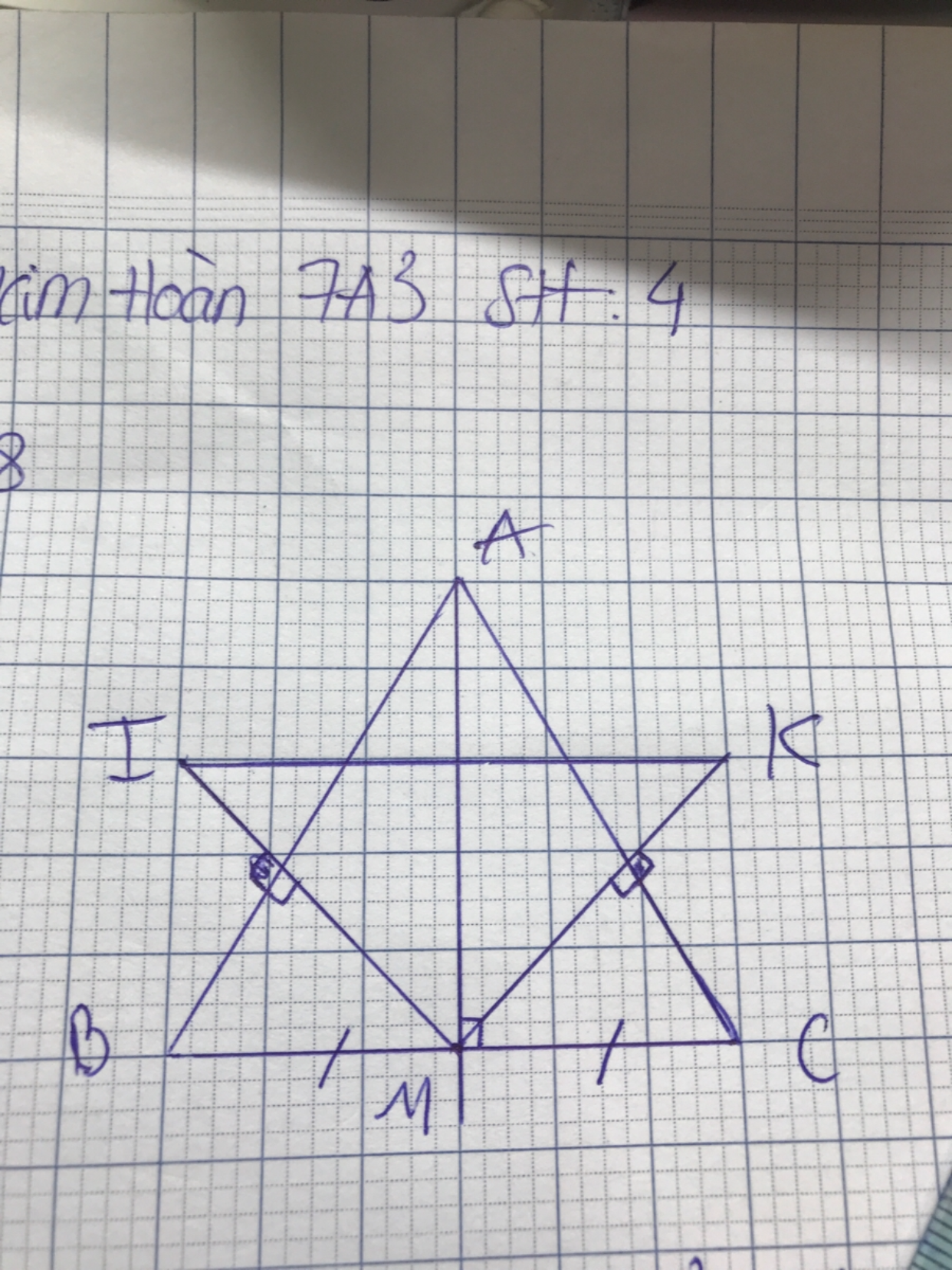 Theo dõi (1) 7 Trả lời
Theo dõi (1) 7 Trả lời -


Cho tam giác ABC vuông ở C, có góc A bằng 60º
bởi Phương Nguyễn Mai
 28/04/2019
28/04/2019
Cho
vuông ở C, có góc A bằng 60º. Tia phân giác của góc BAC cắt BC ở E. Kẻ EK vuông góc với AB (K thuộc AB ). Kẻ BD vuông góc với tia AE (D thuộc tia AE). C/m
a) AC=AK va AE vuông góc CK
b) KA=KB
c)EB>AC
d) Ba đường thẳng AC, BD, KE cùng đi qua một điểm
Theo dõi (0) 4 Trả lời -


Cho
cân tại A, M là trung điểm của BC. Vẽ MH vuông góc với AB (H thuộc AB) vaf MK vuông góc với AC (k thuộc AC). Chứng minh :
a)
b)AH = AK
c) HK // BC
Theo dõi (0) 6 Trả lời -


Cho tam giác ABC cân tại A. Trên tia đối của của BA và CA lấy D và E sao cho: BD=CE
a) CM DE // BC
b) Từ D kẻ DM vg vs BC, Từ E vẽ EN vg vs BC. CM: DM=EN
c)CM tam giác AMN cân
Theo dõi (0) 2 Trả lời -


Chứng minh 3 điểm H, A, E thẳng hàng biết ABM và ACN là tam giác vuông cân
bởi Lê Nhật Minh
 25/02/2019
25/02/2019
Cho tam giác nhọn ABC, đường cao AH. Vẽ ra phía ngoài tam giác đó các tam giác vuông cân tại A là tam giác ABM và tam giác ACN. Gọi E là trung điểm của MN. CMR: 3 điểm H,A,E thẳng hàng. Giúp mình ạ
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABD= tam giác EBD biết tam giác ABC vuông tại A có C=30 độ
bởi Thùy Nguyễn
 22/02/2019
22/02/2019
Cho Δ ABC vuông tại A có góc C = 30° . BD là tia phân giác của góc B ( D € AC) . Kẻ DE vuông góc BC.
a) chứng minh : ΔABD = ΔEBD
b) Chứng minh : Δ ABE là Δ đều
c) so sánh AD và DC
d) Cho AD = √3 cm. Tính AC
Theo dõi (0) 1 Trả lời -


Cho Δ ABC cân tại A. K là trung điểm của BC
a) CM: Δ ABK = Δ ACK
b) CM: AK⊥ BC
c) Vẽ KM ⊥ AB (M ∈ AB), KN ⊥ AC (N ∈ AC)
CM: AB2= MA2+MB2+2MK2Theo dõi (0) 2 Trả lời -


Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC, kẻ HM vuông góc với AB tại M, kẻ AN vuông góc với AC tại N. Chứng minh : AH2+ BM2= AN2+BH2
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABM=tam giác ACM biết AB=AC=10, BC=12, trung tuyến AM
bởi Nguyễn Thanh Trà
 22/02/2019
22/02/2019
cho tam giác ABC có AB=AC=10; BC= 12, vẽ trung tuyến AM
a/ Chững minh tam giác ABM= tam giác ACM
b/ Tính góc AMB
c/ Tính AM
d/ Gọi G là giao của của ba đường trung tuyến, tính AG
Theo dõi (0) 2 Trả lời -


Chứng minh tam giác AMD cân biết AD=AB và AE=AC, đường cao AH cắt ED tại M
bởi minh vương
 26/02/2019
26/02/2019
Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC. Đường cao AH cắt ED tại M
1/ Chứng minh tam giác AMD là tam giác cân.
2/ Chứng minh MA = MD = ME.
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A, M là trung điểm cạnh BC. Vẽ MH vuông góc AB và MK vuông góc AC (H thuộc AB, K thuộc AC). Từ B, vẽ BP vuông góc AC cắt MH tại I. chứng minh rằng
a/ tam giác ABM= tam giác ACM
b/ BH=CK
c/ tam giác IBM cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC , M là trung điểm của BC, biết góc BAM bằng góc CAM. Chứng minh tam giác ABC là tam giác cân
Theo dõi (0) 1 Trả lời -


Chứng minh BD=DC biết tam giác ABC cân tại A, đường thẳng qua B vuông góc AB
bởi hà trang
 22/02/2019
22/02/2019
cho tam giác ABC cân tại A.qua điểm B kẻ đường thẳng vuông góc với AB,qua điểm C kẻ đường thẳng vuông góc với AC chứng cắt tại D.chứng minh:
a, BD = DC
b, AD là tia phân giác của góc A
vẽ hình với nha bạn
Theo dõi (0) 1 Trả lời -


Cho tam giác cân ABC có BM , CN là 2 đường trung tuyến . Chứng mính BM=CN
Theo dõi (0) 1 Trả lời -


Chứng minh MN song song với đường phân giác góc A biết M, N là trung điểm BC, DE
bởi Mai Bảo Khánh
 22/02/2019
22/02/2019
Cho tam giác ABC, AB<AC. Trên hai cạnh AB và AC lấy tương ứng hai điểm D và E sao cho BD=CE. Gọi M, N, I lần lượt là trung điểm của BC, DE, CD. Đường thẳng MN cắt AB và AC theo thứ tự ở P và Q.
Chứng minh:
a) Tam giác MIN là tam giác cân.
b) Tam giác APQ là tam giác cân.
c) MN song song với đường phân giác góc A của tam giác ABC.
Mik vẽ hình rồi mong các bạn giải bài toán giúp mik vs !
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có AB = AC. Gọi D và E là hai đỉnh trên cạnh BC sao cho DB = DE = EC biết AD = AE. Chứng minh:
a) góc EAB= góc DAC
b) BM = MC
c) AM là phân giác của DAE
d) Cho góc DAE = 60o , nhận xét gì về các góc của tam giác AED.
Giúp mk với mn
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A biết C = 70^o
a) tính Góc B và Â
b) So sánh các cạnh của tam giác ABC
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác HAB là tam giác cân biết OH là tia phân giác của góc xOy
bởi Nguyễn Phương Khanh
 22/02/2019
22/02/2019
cho góc nhọn xOy, OH là tia phân giác của góc xOy. Từ H dựng các đường vuông góc xuống hai cạnh Ox và Oy (A thuộc Ox, B thuộc Oy).
a) chứng minh tam giác HAB là tam giác cân
b) gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH. Chứng minh BC vuông góc với Ox
c) khi góc xOy bằng 60 độ. chứng minh OA= 2OD
Theo dõi (0) 1 Trả lời -


Cho \(\Delta\)ABC cân tại A . Kẻ AI \(\perp\)BC , I \(\in\) BC a. Chứng minh : I là trung điểm của BC b. Lấy điểm E \(\in\) AB và điểm F \(\in\) AC sao cho AE = À . Chứng minh : \(\Delta\)IEF là tam giác cân c. Chứng minh : \(\Delta\)EBI = \(\Delta\)FCI
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A (^A< 90độ) kẻ BD vuông góc với BC , CE vuông góc với AB , BD cắt CE tại I chứng minh
a, AD = AE
b, ai là tia phân giác góc BAC
giúp mình nhé mình đang cần gấp
Theo dõi (0) 1 Trả lời -


Cho \(\Delta\)ABC có AB=AC = 5cm , BC = 8cm . Kẻ AH \(\perp\) BC ( H \(\in\)BC ) a. Chứng minh : HB = HC và ^BAH = ^CAH b. Tính độ dài AH c. Kẻ HD \(\perp\) AB ( D \(\in\) AB ) . HE \(\perp\) AC ( E \(\in\) AC ) Chứng minh : \(\Delta\)HDE cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A.Góc A = 20 độ. Trên AB lấy điểm D sao cho AD=BC.Tính góc BDC
Theo dõi (0) 1 Trả lời -


Cho \(\Delta\)ABC cân tại A . Trên tia đối của tia BC và CB lấy theo thứ tự hai điểm Q và R sao cho BQ=CR . a. Chứng minh AQ=AR b. Gọi H là trung điểm của BC . Chứng minh : ^QAH = ^RAH
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 48 trang 127 SGK Toán 7 Tập 1
Bài tập 50 trang 127 SGK Toán 7 Tập 1
Bài tập 51 trang 128 SGK Toán 7 Tập 1
Bài tập 52 trang 128 SGK Toán 7 Tập 1
Bài tập 67 trang 147 SBT Toán 7 Tập 1
Bài tập 68 trang 147 SBT Toán 7 Tập 1
Bài tập 69 trang 147 SBT Toán 7 Tập 1
Bài tập 70 trang 147 SBT Toán 7 Tập 1
Bài tập 71 trang 147 SBT Toán 7 Tập 1
Bài tập 72 trang 147 SBT Toán 7 Tập 1
Bài tập 73 trang 147 SBT Toán 7 Tập 1
Bài tập 74 trang 147 SBT Toán 7 Tập 1
Bài tập 75 trang 147 SBT Toán 7 Tập 1
Bài tập 76 trang 147 SBT Toán 7 Tập 1
Bài tập 77 trang 148 SBT Toán 7 Tập 1
Bài tập 78 trang 148 SBT Toán 7 Tập 1
Bài tập 79 trang 148 SBT Toán 7 Tập 1







