Giải bài 4 tr 12 sách GK Toán Hình lớp 10
Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{0}\)
Hướng dẫn giải chi tiết bài 4
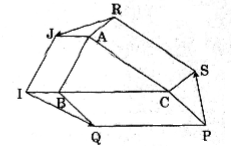
Vì tứ giác ABIJ là hình bình hành, nên \(\overrightarrow {IB} = \overrightarrow {JA} \) , do vậy \(\overrightarrow {IQ} = \overrightarrow {IB} + \overrightarrow {BQ} \) hay \(\overrightarrow {IQ} = \overrightarrow {JA} + \overrightarrow {BQ} \,\,(1)\)
Vì tứ giác BCPQ là hình bình hành, nên \(\overrightarrow {PC} = \overrightarrow {QB} \) do vậy \(\overrightarrow {PS} = \overrightarrow {PC} + \overrightarrow {CS} \,\,hay\,\,\overrightarrow {PS} = \overrightarrow {QB} + \overrightarrow {{\rm{AR}}} \,\,(2)\) (vì \(\overrightarrow {AR} = \overrightarrow {CS} \))
Ta cũng có \(\overrightarrow {RJ} = \overrightarrow {RA} + \overrightarrow {{\rm{AJ}}} \,\,(3)\)
Từ các đẳng thức (1),(2), (3), ta có:
\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow {RA} + \overrightarrow {AJ} + \overrightarrow {JA} + \overrightarrow {BQ} + \overrightarrow {QB} + \overrightarrow {AR} \)
\( = \overrightarrow {RA} + \overrightarrow {AA} + \overrightarrow {BB} + \overrightarrow {AR} \)
\(\begin{array}{l} = \overrightarrow {RA} + \vec 0 + \vec 0 + \overrightarrow {AR} \\ = \overrightarrow {RA} + \overrightarrow {AR} = \overrightarrow {RR} = \vec 0\end{array}\)
-- Mod Toán 10 HỌC247
-


Gọi \(O\) là giao điểm hai đường chéo của hình bình hành \(ABCD\). Chứng minh rằng: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
bởi My Hien
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Gọi \(O\) là tâm của tam giác đều \(ABC\). Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \).
bởi truc lam
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời -


Cho hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) sao cho \(\overrightarrow a + \overrightarrow b = \overrightarrow 0 \). Dựng \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b \). Chứng minh \(O \equiv B\).
bởi Dang Tung
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 12 SGK Hình học 10
Bài tập 3 trang 12 SGK Hình học 10
Bài tập 5 trang 12 SGK Hình học 10
Bài tập 6 trang 12 SGK Hình học 10
Bài tập 7 trang 12 SGK Hình học 10
Bài tập 8 trang 12 SGK Hình học 10
Bài tập 9 trang 12 SGK Hình học 10
Bài tập 10 trang 12 SGK Hình học 10
Bài tập 1.8 trang 21 SBT Hình học 10
Bài tập 1.9 trang 21 SBT Hình học 10
Bài tập 1.10 trang 21 SBT Hình học 10
Bài tập 1.11 trang 21 SBT Hình học 10
Bài tập 1.12 trang 21 SBT Hình học 10
Bài tập 1.13 trang 21 SBT Hình học 10
Bài tập 1.14 trang 21 SBT Hình học 10
Bài tập 1.15 trang 21 SBT Hình học 10
Bài tập 1.16 trang 21 SBT Hình học 10
Bài tập 1.17 trang 21 SBT Hình học 10
Bài tập 1.18 trang 21 SBT Hình học 10
Bài tập 1.19 trang 21 SBT Hình học 10
Bài tập 6 trang 14 SGK Hình học 10 NC
Bài tập 7 trang 14 SGK Hình học 10 NC
Bài tập 8 trang 14 SGK Hình học 10 NC
Bài tập 9 trang 14 SGK Hình học 10 NC
Bài tập 10 trang 14 SGK Hình học 10 NC
Bài tập 11 trang 14 SGK Hình học 10 NC
Bài tập 12 trang 14 SGK Hình học 10 NC
Bài tập 13 trang 15 SGK Hình học 10 NC
Bài tập 14 trang 17 SGK Hình học 10 NC
Bài tập 15 trang 17 SGK Hình học 10 NC
Bài tập 16 trang 17 SGK Hình học 10 NC
Bài tập 17 trang 17 SGK Hình học 10 NC
Bài tập 18 trang 17 SGK Hình học 10 NC





