Bài tập 1.13 trang 21 SBT Hình học 10

37 BT SGK

Giải bài 1.13 tr 21 SBT Hình học 10

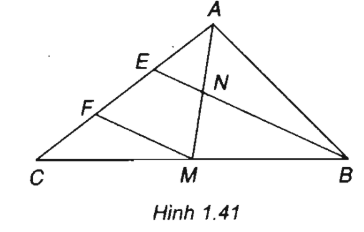
Cho tam giác \(ABC\) có trung tuyến \(AM\). Trên cạnh \(AC\) lấy hai điểm \(E\) và \(F\) sao cho \(AE = EF= FC\); \(BE\) cắt \(AM \) tại \(N\). Chứng minh \(\overrightarrow {NA} \) và \(\overrightarrow {NM} \) là hai vec tơ đối nhau.

Hình học 10 Chương 1 Bài 2 Trắc nghiệm Hình học 10 Chương 1 Bài 2 Giải bài tập Hình học 10 Chương 1 Bài 2

Hướng dẫn giải chi tiết

Giải sách bài tập Toán 10 | Giải sbt Toán 10

Xét tam giác \(CEB,\) ta có:

\(F\) là trung điểm \(CE \) (do \(CF = FE\) )

\(M\) là trung điểm \(CB \)

Suy ra \(FM // BE \) hay \(FM // EN \)

Lại có \(EA = EF\).

\( \Rightarrow EN\) là đường trung bình của tam giác \(AFM\).

Do đó \(N\) là trung điểm của \(AM\) và \(\overrightarrow {NA} = - \overrightarrow {NM} \).

-- Mod Toán 10 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 1.13 trang 21 SBT Hình học 10 HAY thì click chia sẻ

YOMEDIA

Tìm khẳng định sai, biết tam giác ABC có trọng tâm G và trung tuyến AM

bởi bich thu 13/10/2018

Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây sai:

A. \(\overrightarrow{GA}\) + 2. \(\overrightarrow{GM}\) = 0

B. \(\overrightarrow{OA}\) + \(\overrightarrow{OB}\) + \(\overrightarrow{OC}\) = 3. \(\overrightarrow{OG}\) , với mọi điểm O

C. \(\overrightarrow{GA}\) + \(\overrightarrow{GB}\) + \(\overrightarrow{GC}\) = 0

D. \(\overrightarrow{AM}\) = -2 . \(\overrightarrow{MG}\)

Theo dõi (0) 1 Trả lời
Tìm tính chất của tam giác ABC, biết |vt CA+vt CB|=|vt CA- vt CB|

bởi Nguyễn Hồng Tiến 13/10/2018

Tìm tính chất của tam giác ABC, biết\(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=\left|\overrightarrow{CA}-\overrightarrow{CB}\right|\)

Theo dõi (0) 1 Trả lời
Chứng minh vecto AB + vecto CD = vecto AD + vecto CB

bởi Nguyễn Tiểu Ly 13/10/2018

Chứng minh :

Vecto AB + vecto CD = vecto AD + vecto CB

Theo dõi (0) 1 Trả lời