Bài tập 13 trang 15 SGK Hình học 10 NC

a)

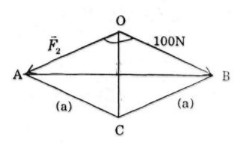
Ta lấy \(\overrightarrow {{F_2}}  = \overrightarrow {OA} ,\overrightarrow {{F_1}}  = \overrightarrow {OB} \).

Theo quy tắc hình bình hành, ta vẽ hình bình hành OACB.

Hình bình hành OACB có OA = OB nên OACB là hình thoi.

Ta có 

\(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  = \overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OC} \),

OC là phân giác góc \(\widehat {AOB}\) nên \(\widehat {AOC} = {60^0}\).

Mà OACB là hình thoi nên tam giác AOC đều. Suy ra OA = OC.

Vậy cường độ lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là 100N.

b)

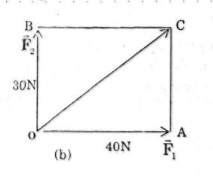
Đặt \(\overrightarrow {OA}  = {\overrightarrow F _1},\overrightarrow {OB}  = \overrightarrow {{F_2}} \). C là đỉnh thứ tư của hình bình hành OABC.

Do góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng 90⁰ suy ra tứ giác OABC là hình chữ nhật.

 \(\begin{array}{l}
 \Rightarrow OC = \sqrt {O{A^2} + O{B^2}} \\
 = \sqrt {{{40}^2} + {{30}^2}}  = 50N
\end{array}\)

Ta có: 

\(\overrightarrow {OC}  = \overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vậy cường độ tổng hợp lực của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là 50N.

-- Mod Toán 10 HỌC247