Giải bài 1.19 tr 21 SBT Hình học 10
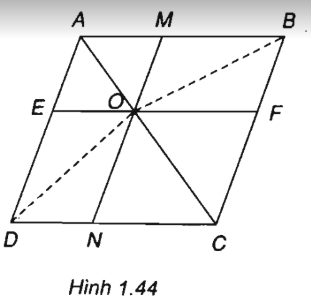
Cho hình bình hành ABCD. Gọi O là một điểm bất kì trên đường chéo AC. Qua O kẻ các đường thẳng song song với các cạnh của hình bình hành. Các đường thẳng này cắt AB và DC lần lượt tại M và N, cắt AD và BC lần lượt tại E và F. Chứng minh rằng:
a) \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \)
b) \(\overrightarrow {BD} = \overrightarrow {ME} + \overrightarrow {FN} \)
Hướng dẫn giải chi tiết
a) \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} ;\overrightarrow {DC} = \overrightarrow {OC} - \overrightarrow {OD} \)
Vì \(\overrightarrow {AB} = \overrightarrow {DC} \) nên ta có \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {OC} - \overrightarrow {OD} \)
Vậy \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \)
b) Tứ giác AMOE là hình bình hành nên ta có \(\overrightarrow {ME} = \overrightarrow {MA} + \overrightarrow {MO} \) (1)
Tứ giác OFCN là hình bình hành nên ta có \(\overrightarrow {FN} = \overrightarrow {FO} + \overrightarrow {FC} \) (2)
Từ (1) và (2) suy ra :
\(\begin{array}{l}
\overrightarrow {ME} + \overrightarrow {FN} = \overrightarrow {MA} + \overrightarrow {MO} + \overrightarrow {FO} + \overrightarrow {FC} \\
= \left( {\overrightarrow {MA} + \overrightarrow {FO} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {FC} } \right) = \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD}
\end{array}\)
(Vì \(\overrightarrow {FO} = \overrightarrow {BM} ,\overrightarrow {MO} = \overrightarrow {BF} \))
Vậy \(\overrightarrow {BD} = \overrightarrow {ME} + \overrightarrow {FN} \)
-- Mod Toán 10 HỌC247
-


Bài 1.16 trang 23 sách bài tập Hình học 10
bởi Nguyễn Thanh Thảo
 02/10/2018
Bài 1.16 (STB trang 23)
02/10/2018
Bài 1.16 (STB trang 23)Cho ngũ giác ABCDE. Chứng minh \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AE}-\overrightarrow{DE}\) ?
Theo dõi (0) 1 Trả lời -


Bài 1.15 trang 23 sách bài tập Hình học 10
bởi Nguyễn Vũ Khúc
 02/10/2018
Bài 1.15 (STB trang 23)
02/10/2018
Bài 1.15 (STB trang 23)Cho tam giác ABC. Chứng minh rằng nếu \(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=\left|\overrightarrow{CA}-\overrightarrow{CB}\right|\) thì tam giác ABC là tam giác vuông tại C ?
Theo dõi (0) 1 Trả lời -


Bài 1.14 trang 23 sách bài tập Hình học 10
bởi Lê Minh
 02/10/2018
Bài 1.14 (STB trang 23)
02/10/2018
Bài 1.14 (STB trang 23)Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau :
a) \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\)
b) \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\)
c) \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.17 trang 21 SBT Hình học 10
Bài tập 1.18 trang 21 SBT Hình học 10
Bài tập 6 trang 14 SGK Hình học 10 NC
Bài tập 7 trang 14 SGK Hình học 10 NC
Bài tập 8 trang 14 SGK Hình học 10 NC
Bài tập 9 trang 14 SGK Hình học 10 NC
Bài tập 10 trang 14 SGK Hình học 10 NC
Bài tập 11 trang 14 SGK Hình học 10 NC
Bài tập 12 trang 14 SGK Hình học 10 NC
Bài tập 13 trang 15 SGK Hình học 10 NC
Bài tập 14 trang 17 SGK Hình học 10 NC
Bài tập 15 trang 17 SGK Hình học 10 NC
Bài tập 16 trang 17 SGK Hình học 10 NC
Bài tập 17 trang 17 SGK Hình học 10 NC
Bài tập 18 trang 17 SGK Hình học 10 NC