Bài tập 1.15 trang 21 SBT Hình học 10

37 BT SGK

Giải bài 1.15 tr 8 SBT Hình học 10

Cho tam giác \(ABC\). Chứng minh rằng nếu \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right|\) thì tam giác \(ABC\) là tam giác vuông tại \(C\).

Hình học 10 Chương 1 Bài 2 Trắc nghiệm Hình học 10 Chương 1 Bài 2 Giải bài tập Hình học 10 Chương 1 Bài 2

Hướng dẫn giải chi tiết

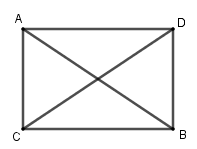
Vẽ hình bình hành \(CADB\). Ta có \(\overrightarrow {CA} + \overrightarrow {CB} = \overrightarrow {CD} \), do đó \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = CD\)

Vì \(\overrightarrow {CA} - \overrightarrow {CB} = \overrightarrow {BA} \), Do đó \(\left| {\overrightarrow {CA} - \overrightarrow {CB} } \right| = BA\).

Từ \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right|\) suy ra \(CD = AB\)

Vậy tứ giác \(CADB\) là hình chữ nhật. Ta có tam giác \(ABC\) vuông tại \(C\).

-- Mod Toán 10 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 1.15 trang 21 SBT Hình học 10 HAY thì click chia sẻ

YOMEDIA

Tính độ dài vecto AB+ vecto AD biết hình chữ nhật ABCD có AB=4a, AD=3a

bởi Bánh Mì 16/10/2018

Câu 1. Cho hình chữ nhật ABCD Biêt AB=4a AD=3a Thì độ dài \(\overrightarrow{AB}\) + \(\overrightarrow{AD}\)bằng

Theo dõi (0) 1 Trả lời
Rút gọn vecto AB-vt CB+ vt CD-vt ED

bởi thi trang 16/10/2018

1) Rút gọn biểu thức : vecto AB-vt CB+ vt CD-vt ED
2) trong mặt phảng OXY, cho tam giác G của tam giác ABC
a) Tìm vtAB và trọng tâm G của tam giác ABC
b) Tìm tọa độ D sao cho vtCD=2vtAB
c) Tính vtCA* vtBC
d) Tính chu vi và diện tích tam giác ABC
e) tính góc B của tam giác ABC
f) Tìm tọa độ điểm E thuộc õ sao cho

Theo dõi (0) 1 Trả lời
Chứng minh vt RJ+vt IQ+vt PQ= vt 0

bởi Hoa Lan 22/10/2018

1. Cho hbh ABCD và một điểm M tuỳ ý. Cmr: vecto MA + MC= MB+MD

2. Cho tam giác ABC bên ngoài tam giác vẽ hbh ABIJ BCPQ CARS. Cmr: vecto RJ + IQ + PD= vecto 0

3. Cho 3 điểm O A B ko thẳng hàng. Với điều kiện nào vecto OA + OB nằm trên đường phân giác của góc AOB

Theo dõi (0) 1 Trả lời