Giải bài 76 tr 51 sách BT Toán lớp 7 Tập 2
Cho tam giác \(ABC\) cân tại \(A,\) đường trung tuyến \(AM.\) Qua \(A\) kẻ đường thẳng \(d\) vuông góc với \(AM.\) Chứng minh rằng \(d\) song song với \(BC.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Trong một tam giác cân, đường trung tuyến ứng với cạnh đáy cũng đồng thời là đường phân giác, đường trung trực và đường cao của tam giác đó.
+) Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Lời giải chi tiết
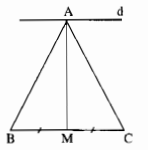
∆ABC cân tại A, AM là đường trung tuyến nên AM cũng là đường cao.
\(\eqalign{
& {\rm{AM}} \bot {\rm{BC}} \cr
& {\rm{d}} \bot {\rm{AM}}\left( {gt} \right) \cr} \)
Suy ra: d // BC (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba).
-- Mod Toán 7 HỌC247
-


Chứng minh ME=MF, AE=AF biết E, F là chân đường vuông góc kẻ từ M đến AB, AC
bởi Thụy Mây
 27/02/2019
27/02/2019
cho tam giac ABC can tai A. Goi M la chung diem cua BC .Goi E,F thu tu la chan cac duong vuong goc ke tu M den AB vaAC.Chung minh ME=MF AE=AF ,AM vuong goc EF ,EF//BC
Theo dõi (0) 1 Trả lời -


Đề kiểm tra 1 tiết hình chương 1 Toán 7
bởi hành thư
 27/02/2019
27/02/2019
ai co de kiem tra 1 tiet hinh chuong 1 khong
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác BHC cân biết tam giác ABC cân tại A có các đường cao BD, CE
bởi Bo Bo
 27/02/2019
27/02/2019
Cho \(\Delta ABC\)cân tại A \(\left(\widehat{A}< 90^0\right)\);các đường cao BD; CE cắt nhau tại H.
a) Chứng minh: \(\Delta ABD=\Delta ACE\).
b) Chứng minh: \(\Delta BHC\)là tam giác cân.
c) So sánh HB và HD.
d) Trên tia đối của tia EH lấy điểm N sao cho NH < HC. Trên tia đối của tia DH láy ddiemr M sao cho MH = NH. Chứng minh các đường thẳng BN; AH; CM đồng quy.
Theo dõi (0) 1 Trả lời -


cho tam giác ABC có góc A=900 và AB=AC. gọi H là trung điểm của BC. Chứng minh rằng:
a/ tam giác AHB= tam giác AHC
b/ AH vuông góc với BC
Theo dõi (0) 1 Trả lời -


Bài tập hình lớp 7 nâng cao chương 1
bởi Nguyễn Hồng Tiến
 28/02/2019
28/02/2019
Các bạn ơi. Mình thấy hình học lớp 7 khó quá. Các bạn có cách nào để học tốt nó không???
Các bạn tìm giúp mình mấy bài toán hình lớp 7 nâng cao ở chương 1 luôn nha\
Cảm ơn mấy bạn rất nhiều
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A, đường cao AD. Biết AB=10 cm; BC= 12 cm
a/tính độ đài đoạn thẳng BD, AD
b/ gọi G là trọng tâm của tam giác ABC. Chứng minh ba điểm A,G,D thẳng hàng
c/ chứng minh tam giác ABG = tam giác ACG
Theo dõi (0) 1 Trả lời -


Làm thế nào để dễ phân biệt giữa đường trung trực, đường trung tuyến và đường cao?
bởi Lan Anh
 28/02/2019
28/02/2019
Cho mềnh hỏi: Làm thế nào để dễ phân biệt nhất giữa đường trung trực, đường trung tuyến và đường cao vậy??
Theo dõi (0) 1 Trả lời -


Cm H; G; O thẳng hàng biết H; G; D là trục tâm, trọng tâm, giao điểm trung trực tam giác ABC
bởi Naru to
 28/02/2019
28/02/2019
Cho tam gác ABC, gọi H; G; D lần lượt là trục tâm, trọng tâm, giao điểm trung trực của tam giác đó. c/m:
a) AH là 2 lần khoảng cách từ O đến BC.
b) c/m H; G; O thẳng hàng và GH= 2GO.
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A, có 2 đường phân giác BD và CF cắt nhau ở H, 2 đường trung tuyến BM và CQ cắt nhau ở G.
1) G là điểm gì của tam giác ABC. CM: G thuộc đường cao của tam giác ABC.
2) A, G, H thẳng hàng
Theo dõi (0) 1 Trả lời -


cho tam giác ABC, ba đường cao AD,BE,CF.biết AD=BD=CF. chứng minh tam giác ABC là tam giác đều
Theo dõi (0) 1 Trả lời -


Chứng minh AC=AK và AE vuông CK biết tam giác ABC vuông ở C có A=60 độ
bởi Nguyễn Thanh Hà
 22/02/2019
22/02/2019
Cho \(\Delta\) ABC vuông ở C có góc A = 60\(^o\). Tia phân giác của \(\widehat{BAC}\) cắt BC ở E. Kẻ EK \(\perp\) AB (K \(\in\) AB). Kẻ BD \(\perp\) tia AE (D \(\in\) AE). Cm :
a) AC = AK và AE \(\perp\) CK.
b) KA = KB.
c) EB > AC.
d) Ba đường thẳng AC, BD, KE cùng đi qua một điểm.
Theo dõi (0) 1 Trả lời -


Gọi a;b;c là các cạnh tam giác; 3 đường cao tương ứng là \(h_a;h_b;h_c\).
CMR \(\dfrac{\left(a+b+c\right)^2}{h_a^2+h_b^2+h_c^2}\ge\text{4}\).
Theo dõi (0) 1 Trả lời -


Chứng minh BE vuông góc KC biết tam giác ABC vuông tại A, EH vuông BC
bởi Lê Trung Phuong
 01/03/2019
01/03/2019
Cho Δ ABC vuông tai A. Có phân giác BE. Kẻ EH vuông góc với BC (H ϵ BC). Gọi K là giao điểm của các cạnh BA và HE.
a) Chứng minh: BE ⊥ KC
b) So sánh AE và EC
c) Lấy D thuộc cạnh BC, sao cho góc BAD=\(^{45^0}\). Gọi I là giao điểm của BE và AD. Chứng minh I cách đều ba cạnh của tam giác ABC
giúp mk với ạ.:((
Theo dõi (0) 1 Trả lời -


Chứng minh CH vuông góc BD biết đường thẳng d vuông góc BC cắt AB tại H
bởi Lê Trung Phuong
 01/03/2019
01/03/2019
Cho tam giác ABC vuông tại A. Từ điểm M trên cạnh BC vẽ đường thẳng d\(\perp BC\) cắt cạnh AB tại H và cắt đường AC tại D. Chứng minh\(CH\perp BD\)
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC có các đường cao BD và CE bằng nhau là tam giác cân
bởi Phan Thiện Hải
 25/02/2019
25/02/2019
Cho tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng tam giác đó là tam giác cân
Theo dõi (0) 1 Trả lời -


Chứng minh M là trực tâm tam giác ANB biết M và N lần lượt là trung điểm của AH và CH
bởi Lê Tấn Thanh
 25/03/2019
25/03/2019
cho tam giác ABC vuông tại A, đường cao AH. Gọi M và N lần lượt là trung điểm của AH và CH. Chứng minh
a, M là trực tâm của tam giác ANB
b,BM\(\perp\)AN
Theo dõi (0) 1 Trả lời -


tính cạnh đáy của tam giác cân trong hình sau
Theo dõi (0) 1 Trả lời -


Chứng minh OK vuông góc DE biết NA vuông góc với Ox, NB vuông góc với Oy
bởi Nguyễn Quang Thanh Tú
 28/03/2019
28/03/2019
cho góc nhọn xOy và N là 1 điểm thuộc tia phân giác của góc xOy. Kẻ NA vuông góc với Ox ( a thuộc Ox), NB vuông góc với Oy( B thuộc Oy)
a. C/m: NA=NB
b. Tam giác OAB là tam giác gì? Vì sao?
c. Đường thẵng BN cắt Ox tại D, đường thẳng AN cắt Oy tại E. C/m: ND=Ne
d. C/m: OK⊥DE
Mọi người làm ơn giúp mk đi, mk cảm ơn trước nha :) !Theo dõi (0) 1 Trả lời -


Chứng minh P là trực tâm tam giác BẢ biết trên AH lấy điểm P sao cho PH=BH
bởi Đan Nguyên
 26/03/2019
Cho tam giác ABC vuông tại A. Vẽ đường cao AH. Trên AH lấy điểm P sao cho PH=BH. Trên HC lấy điểm R sao cho HR=AH. CM: P là trực tâm của ΔBARTheo dõi (0) 1 Trả lời
26/03/2019
Cho tam giác ABC vuông tại A. Vẽ đường cao AH. Trên AH lấy điểm P sao cho PH=BH. Trên HC lấy điểm R sao cho HR=AH. CM: P là trực tâm của ΔBARTheo dõi (0) 1 Trả lời -


cho góc nhọn xOy trên tia Ox xác định hai điểm A , B sao cho A nằm giữa hai điểm O và B trên tia Oy xác định hai điểm C và D sao cho OC =OA , OD = OB gọi I là giao điểm của AD và BC chứng minh rằng
a) AD = BC
b) AI = IC
c) OI ⊥ BD
Theo dõi (0) 1 Trả lời -


Bài 61 trang 83 SGK Toán 7 tập 2
bởi Phan Thiện Hải
 25/02/2019
25/02/2019
Câu 61: Trang 83 - SGK Toán 7 tập 2
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) vuông cân tại A, gọi \(D,E\) là 2 điểm theo thứ tự nằm trên AB, AC sao cho AD = AE. Gọi K là điểm thuộc BC. Trên nửa mặt phẳng bờ AC k chứa điểm B vẽ I sao cho \(\widehat{EAI}=\widehat{DAK}\) và \(AI=AK\) C/m \(KE+KD\ge AB\)
Theo dõi (0) 1 Trả lời -


Tam giác ABC đều có cạnh bằng 10cm Tính độ dài đường cao của Tam giác xuất phát từ A
Theo dõi (0) 1 Trả lời -


Hãy giải thích vì sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác
Theo dõi (0) 1 Trả lời





