Giải bài 74 tr 51 sách BT Toán lớp 7 Tập 2
Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Tìm trực tâm của tam giác \(ABC, AHB, AHC.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng: Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.
Lời giải chi tiết
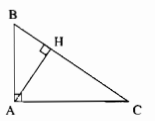
∆ABC có \(\widehat {BAC} = 90^\circ \)
CA là đường cao xuất phát từ đỉnh C. BA là đương cao xuất phát từ đỉnh B. Giao điểm của hai đường này là A. Vậy A là trực tâm của ∆ABC.
∆AHB có \(\widehat {AHB} = 90^\circ \)
AH là đường cao xuất phát từ đỉnh A; BH là là đường cao xuất phát từ đỉnh B. Giao điểm của hai đường này là H. Vậy H là trực tâm của ∆AHB
∆AHC có \(\widehat {AHC} = 90^\circ \)
AH là đường cao xuất phát từ đỉnh A; CH là đường cao xuất phát từ đỉnh C. Giao điểm của hai đường này là H
Vậy H là trực tâm của ∆AHC.
-- Mod Toán 7 HỌC247
-

cho tam giác ABC vuông tại A có AB < AC và AH vuông góc với BC, lấy D trên Ac sao cho AB = AD. Vẽ DE vuông góc với BC, DK vuông góc với AH
CMR: a) HA = KD
b) Tam giác HAE vuông cân
Theo dõi (0) 0 Trả lời -


Bài 1: Cho tam giác ABC cân tại A, lấy M là trung điểm của BC.
a, Chứng minh AM vuông góc với BC.
b, Kẻ ME vuông góc với AB tại E, MF vuông góc với AC tại F. chứng minh rằng ME = MF
c, Chứng minh rằng: EF//BC
d, Tia EM cắt AC tại K. Tia FM cắt AB tại H. Tìm điều kiện của tam giác ABC để tam giác AHK đều.
Bài 2: Cho tam giác ABC cân tại B, kẻ AI là tia phân giác của góc BAC , IH vuông góc AC tại H
a, Chứng minh tam giác ABI = tam giác AHI
b, HI cắt AB tại K. Chứng tỏ rằng: BK = HC
c, Chứng minh rằng: BH//KC
d, Qua C kẻ đường thẳng song song với HK, cắt AI tại O. Tìm điều kiện của tam giác ABC để tam giác CIO đều.
Bài 3: Cho tam giác DEF cân có DE = DF = 5cm, EF = 8cm. Kẻ DK vuông góc EF tại F
a, Chứng minh rằng KE = KF
b, Tính độ dài DK
Giúp mik vs, vẽ hình và viết giả thiết và kết luận lun nhaz!!! Hơi cực 1 xíu, cho mik XL
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

Cho tam giác ABC, m là trung điểm của BC. Trên tia đối của MA lấy E sao cho ME = MA
bởi Nguyễn Tuấn Anh
 29/01/2019
29/01/2019
Cho tam giác ABC, m là trung điểm của BC. Trên tia đối của MA lấy E sao cho ME = MA
a) Cmr: Tam giác AMB = Tam giác EMC
b) Cmr: AB//CE
c) Gọi I là trung điểm của AC. Trên tia đối của IB lấy K sao cho IB = IK. Cmr: E, C, K thẳng hàng
Theo dõi (0) 0 Trả lời -


So Sánh 2018^2017 và 2017^2018
bởi Lâm Tử Nhi
 29/01/2019
29/01/2019
So sánh:
và
Theo dõi (0) 1 Trả lời -


Cho góc nhọn xOy gọi Ot là tia phân giác của góc xOy, lấy điểm M thuộc Ot
bởi Lê Khánh Linh
 27/01/2019
27/01/2019
Cho góc nhọn xOy gọi Ot là tia phân giác của góc xOy, lấy điểm M thuộc Ot. Kẻ MA vuông góc với Ox tại A, kẻ MB vuông góc với Oy tại B
1/ Chứng minh MA = MB
2/Cho OA=8cm; OB=10cm Tính độ dài của MA.
3/Tia OM cắt AB tại I. Chứng minh: OM là đường trung trực của đoạn thẳng AB
Theo dõi (0) 2 Trả lời -


Tam giác ABC có M thuộc cạnh AC, D thuộc tia đối của tia MB Chứng minh AD+BC < AC+BD
bởi Giang Kì
 25/01/2019
25/01/2019
Tam giác ABC có M thuộc cạnh AC, D thuộc tia đối của tia MB Chứng minh AD+BC < AC+BD
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC có ba góc đều nhọn, AB
bởi Bùi Văn Linh
 21/01/2019
21/01/2019
Cho tam giác ABC có ba góc đều nhọn, AB<AC. vẽ AH vuông góc với BC (H thuộc BC). Trên tia AH lấy điểm K sao cho H là trung điểm của AK.
a)Chứng minh rằng: Tam giác ACH bằng tam giác KCH
b)gọi E là trung điểm của BC. Trên tia AE lấy điểm D sao cho E là trung điểm của AD.
chứng minh rằng BD = AC = CK
c) Chứng minh EH là phân giác của góc AEK và DK // BC
d) Gọi I là giao điểm của BD và CK, N là trung điểm của KD. chứng minh ba điểm E, I , N thẳng hàng.
Theo dõi (1) 0 Trả lời -


Cho tam giac ABC , M là điểm nằm giữa B và C
bởi Ngoc Ha
 20/01/2019
20/01/2019
cho tam giac ABC , M là điểm nằm giữa B và C. CMR
a) Nếu MB=MC và AM=BC thì AB=AC
b) Nếu AM vuông góc BC và <BAM=<CAM thì AB =AC
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC có góc B bằng 75 độ, góc C bằng 60 độ. Trên tia đối của tia CB lấy điển D sao cho CD bằng 1/2 BC. Tính số đó góc ADB
Các bạn giúp dùm mình nhé
Theo dõi (0) 0 Trả lời -

Cho tam giác MNP có góc M = 90 độ. Phân giác của góc N cắt MP tại I. Trên NP lấy K sao cho MN = NK.
Chứng minh rằng :
a) MI=IR
b)góc MNP= góc KID
c) MK vuông góc với NI
Theo dõi (0) 0 Trả lời -

Cho tam giác ABC có Ab < Ac. Gọi AD là phân giác của góc BAC. Trên AC lấy E sao cho AB=AE.
bởi Nguyễn Tuấn Anh
 30/11/2018
30/11/2018
Cho tam giác ABC có Ab < Ac. Gọi AD là phân giác của góc BAC. Trên AC lấy E sao cho AB=AE.
Chứng minh rằng :
a) BD = DE
b) AD là trung trực DE
Theo dõi (0) 1 Trả lời -


Chứng minh x+2y chia hết cho 5 khi và chỉ khi 3x-4y chia hết cho 5
bởi Nguyễn Thị Linh Chi
 29/11/2018
29/11/2018
cmr x+2y chia hết cho 5 khi và chỉ khi 3x-4y chia hết cho 5
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, kẻ BD vuông góc AC, CE vuông góc với AB. trên tia đối của tia BD, lấy điểm H SAO CHO bh=ac. TRÊN TIA ĐỐI của tia CE, lấy điểm K sao cho CK=AB. chứng minh rằng AM=AK
bởi Nguyễn Thị Linh Chi
 29/11/2018
29/11/2018
BÀI 1cho tam giác ABC, kẻ BD vuông góc AC, CE vuông góc với AB. trên tia đối của tia BD, lấy điểm H SAO CHO bh=ac. TRÊN TIA ĐỐI của tia CE, lấy điểm K sao cho CK=AB. chứng minh rằng AM=AK
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, vẽ về phía ngoài của tam giác các tam giác vuông tại A là ABD, ACE có AB=AD và AC=A
bởi Nguyễn Thị Phương Hiền
 29/11/2018
29/11/2018
cho tam giác ABC, vẽ về phía ngoài của tam giác các tam giác vuông tại A là ABD, ACE có AB=AD và AC=AE. kẻ AH vuông BC tại H, DM vuông AH tại M, ENvuông AH tại N. Cmr:
a) DM=AH
b) MN đi qua trung điểm của DE
Theo dõi (0) 0 Trả lời -


cho tam giác ABC nhọn. vẽ đoạn AD vuông góc với ABvà bằng AB(Dkhác phía C đối với AB),vẽ đoạn thẳng AE vuông góc với AC(Ekhác phía B đối với AC) cmr
a)DC=BE
b)DC vuông BE
Theo dõi (0) 4 Trả lời -


Cho tam giác ABC vuông tại A, M là trung điểm của cạnh BC. C/minh AM = 1/2 BC
bởi Hoàng Thụy Linh
 22/11/2018
22/11/2018
a. Cho tam giác ABC vuông tại A, M là trung điểm của cạnh BC. C/minh AM = 1/2 BC.
b. Cho tam giác ABC, gọi M, N lần lượt là trung điểm của AB, AC. C/minh rằng MN // BC cà MN =1/2.
Theo dõi (0) 1 Trả lời -


Cho góc nhọn xOy, trên tai Ox lấy điểm A, C, trên tia Oy lấy điểm B, D, sao cho OA = OB, OC =OD
bởi Hoàng Thụy Linh
 22/11/2018
22/11/2018
Cho góc nhọn xOy, trên tai Ox lấy điểm A, C, trên tia Oy lấy điểm B, D, sao cho OA = OB, OC =OD.
a. C/minh: tam giác OAD = tam giác OBC.
b. C/minh góc CAD = góc CBD.
Theo dõi (0) 1 Trả lời -


Tam giác ABC có đường cao AH và trung tuyến AM chia góc A thành 3 góc bằng nhau
bởi ミ★Bạch Kudo★彡
 21/11/2018
21/11/2018
Tam giác ABC có đường cao AH và trung tuyến AM chia góc A thành 3 góc bằng nhau. Chứng minh rằng tam giác ABC vuông và tam giác ABM là tam giác đều.
--- Trình bày lời giải rõ ràng, hợp lí và dễ hiểu => like cho ---
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có ba góc nhọn, AB < AC gọi M là trung điểm cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD= MA
a) Chứng minh tam giác ABM = tam giác DCM
b) Chứng minh BD // AC
c) Kẻ AH vuông góc BC tại H; kẻ DK vuông góc BC tại K chứng minh M là trung điểm của đoạn HK
Theo dõi (0) 1 Trả lời -


1. Cho tam giác ABC vuông tại A có góc C = 30 độ . Trên tia BA lấy E sao cho BE = BC . Tia phân giác của góc B cắt AC tại I
a) Chứng minh tam giác BEC đều .
b) Chứng minh IE = IC
c) Chứng minh IE vuông góc với BC .
HELP ME !!!!!!!!!!
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC , M là trung điểm BC .Kẻ từ BI, CF vuông góc với AM( I,F thuộc tia AM) CM : BI= CF
Chủ yếu là vẽ hình ai vẽ hình mình bái phục
Theo dõi (0) 1 Trả lời -


Tính độ dài mỗi cạnh tam giác có diện tích là 60cm^2 và độ dài các đường cao
bởi Nguyễn Thủy Tiên
 26/02/2019
26/02/2019
diện tích của tam giác là 60 cm vuông. Các đường cao có độ dài là 12cm, 15cm , 20cm. tính độ dài mỗi cạnh
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A (A<\(90^0\)) các đường cao BD, CE(D\(\in\)AC, E\(\in\)AB) cắt nhau tại H.
a, cm △ABD=△ACB,
B, △BHC là tam giác cân
c, so sánh HB và HD
d, trên tia đối của ta EH lấy điểm N sao cho NH<HC; trên tia đối của tia DH lấy điểm M sao cho MH=NH. CM các đường thẳng BN, AH, CM đồng quy
Theo dõi (0) 1 Trả lời -


Chứng minh BC đi qua trung điểm của KN biết đường cao BH và CK cắt nhau tại M
bởi Aser Aser
 26/02/2019
26/02/2019
1. Cho tam giác ABC cân tại A. Đường cao BH và CK cắt nhau ở M
a) CM: BH=CK
b) tam giác BMC cân
c) KH//BC
d) Trên tia đối của tia CA lấy N sao cho: CH=CN. Cm: BC đi qua trung điểm của KN
e) Qua B kẻ đường thẳng vuông góc với BC cắt CK ở I. Cm: góc IBK= góc HAM
Bài 1 em chỉ k biết làm câu d và e
Theo dõi (0) 1 Trả lời






