Giải bài 81 tr 51 sách BT Toán lớp 7 Tập 2
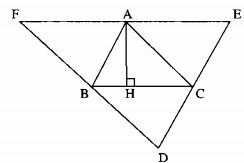
Cho tam giác \(ABC.\) Qua mỗi đỉnh \(A, B, C\) kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác \(DEF\) (h.17)
a) Chứng minh rằng \(A\) là trung điểm \(EF.\)
b) Các đường cao của tam giác \(ABC\) là các đường trung trực của tam giác nào?
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Tính chất hai tam giác bằng nhau
+) Quan hệ từ vuông góc đến song song
+) Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm đoạn thẳng ấy.
Lời giải chi tiết
a) Xét ∆ABC và ∆ACE:
\(\widehat {ACB} = \widehat {CA{\rm{E}}}\) (so le trong, AE // BC)
AC cạnh chung
\(\widehat {CAB} = \widehat {AC{\rm{E}}}\) (so le trong, CE // AB)
Do đó: ∆ABC = ∆CEA (g.c.g)
\( \Rightarrow \) AE = BC (1)
Xét ∆ABC và ∆ABF:
\(\widehat {ABC} = \widehat {{\rm{BAF}}}\) (so le trong, BF // AC)
AC cạnh chung
\(\widehat {BAC} = \widehat {ABF}\) (so le trong, BF // AC)
Do đó: ∆ABC = ∆BAF (g.c.g)
\( \Rightarrow \) AF = BC (2)
Từ (1) và (2) suy ra: AE = AF. Vậy A là trung điểm EF.
b) Kẻ \({\rm{A}}H \bot BC\)
EF // BC (gt)
\( \Rightarrow \) \(AH \bot EF\)
AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Chứng minh tương tự câu a, ta có B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ∆ABC là đường trung trực DFF.
Ta có C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ∆ABC là đường trung trực của DE.
-- Mod Toán 7 HỌC247
-
Cho tam giác ABC, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD=MA
bởi Hồ Nhật Anh
10/04/2018
Cho tam giác ABC, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD=MA
- Chứng minh AB // CD và AB = CD; AC // BD và AC = BD
- Gọi E và F lần lượt là trung điểm của AC và BD; AF cắt BC tại I, DE cắt BC tại K
Chứng minh: BI = IK = KC
Theo dõi (0) 0 Trả lời -
Cho ΔABC cân tại A, gọi 2 điểm M,N lần lượt là trung điểm của AB và AC
bởi Manhtan Nguyen
10/04/2018
Cho ΔABC cân tại A, gọi 2 điểm M,N lần lượt là trung điểm của AB và AC. Hai đoạn BN và CM cắt nhau tại G.
a) Chứng minh AM=AN
b) Trên tia đối tia NB, lấy điểm K sao cho NK=NG. Chứng minh ΔANG=ΔCNK. Từ đó suy ra AG//CK
c) Chứng minh BG=GK
d) Chứng minh: BC+AG>2GK
Theo dõi (0) 0 Trả lời -
Cho tam giác ABC vuông tại A, đường cao AH
bởi Nguyễn Thị Lan
04/04/2018
Chỉ mình với các bạn ơi!
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD=BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh:
a, Tam giác ABE=DBE.
b, BE là đường trung trực của đọan AD.
c, Tia BE là phân giác của góc ABC.
d, Tam giác CEF là tam giác cân.
e, BE vuông CF.
f, HD< DC.
Theo dõi (0) 2 Trả lời -
Cho △MNP cân tại M(góc NMP <90 độ
bởi Trần Thảo
01/04/2018
Cho △MNP cân tại M(góc NMP <90 độ)Kẻ ND⊥MP(D∈MP),PE⊥MN(E∈MN),ND và PE cắt nhau tại H
a)Chứng minh ND=PE
b)Chứng minh △NHP cân
c)Chứng minh MH là đường trung trực của NP
d)Trên tia ND lấy điểm K sao cho D là trung điểm của NK.So sánh góc MKN và góc MPE
Theo dõi (0) 1 Trả lời -
Cho hai đt xx’ và yy’ cắt nhau tại O, Ox, Ox’ lần lượt lấy các điểm B, D sao cho OA = OB, OC = OD
bởi bich thu
29/03/2018
Ai đó giúp em với
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Trên Ox, Ox’ lần lượt lấy các điểm B, D sao cho OA = OB, OC = OD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh M, O, N thẳng hàng.
Theo dõi (0) 2 Trả lời -
Cho đt x'x và O nằm trên đt ấy, Oy vuông góc với x’x, D là hình chiếu của A trên đường thẳng BC
bởi thu thủy
28/03/2018
Giúp em bài này với ạ
Cho đường thẳng x'x và một điểm O nằm trên đường thẳng ấy. Dựng tia Oy vuông góc với x’x. Trên tia Oy lấy hai điểm A và B nào đó sao cho A nằm giữa O và B, trên tia Ox lấy một điểm C nào đó. Gọi D là hình chiếu của A trên đường thẳng BC.
a. Chứng tỏ rằng hai đường thẳng x’x và AD cắt nhau tại điểm E.
b. Chứng minh: \(AC \bot BE\)
c. Chứng minh rằng hai góc BAE và BCE bù nhau (tổng số đo hai góc bằng 1800).
Theo dõi (0) 2 Trả lời -
Minh đem ra cửa hàng1 số tiền và nhẫm tính nếu dùng số tiền ấy có thể mua đc 2 kg nho,hoặc 3 kg lê
bởi Lee Ngân
09/03/2018
Minh đem ra cửa hàng1 số tiền và nhẫm tính nếu dùng số tiền ấy có thể mua đc 2 kg nho,hoặc 3 kg lê,hoặc 5 kg cam. Biết rằng giá tiền 2 kg lê thì đắt hơn 3 kg cam là 4 nghìn đồng.Tính giá tiền 1 kg mỗi loại
Theo dõi (0) 1 Trả lời -
HÌNH HỌC LỚP 7
bởi Lee Ngân
09/03/2018
Cho tam giác ABC vuông tại A ,đường trung tuyến AM.Qua A kẻ đường thẳng d vuông góc với AM.Qua M kẻ đường thẳng vuông góc với AB và AC , chúng cắt d theo thứ tự ở D và E . Chứng minh rằng :
a)BD//CE
b)DE=BD+CE
Theo dõi (1) 1 Trả lời -
cho tam giác ABC có C=90 A=30 ÁC=10 cm kẻ CD vuông góc vs AB DE vuông góc vs AC tính độ dài AE
bởi Ngô Xuân Phương
02/03/2018
cho tam giác ABC có C=90 A=30 ÁC=10 cm kẻ CD vuông góc vs AB DE vuông góc vs AC tính độ dài AE
Theo dõi (2) 2 Trả lời -
Cho tam giác ABC có Â=40độ, AB=AC.
bởi Trần quỳnh Trang
28/02/2018
Cho tam giác ABC có Â=40độ, AB=AC. Gọi H là trung điểm BC a) Tính góc ABC, ACB b) C/m: AH vuông góc BC c) Trung trực của AC cắt CB tại M. Tính MÂH d) Trên tia đối AM lấy N sao cho AN=BM. C/m: AM=CN e) Vẽ CI vuông góc MN tại I. C/m: I là trung điểm MN
Theo dõi (1) 1 Trả lời -
Trọng tâm, trực tâm, tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp trong tam giác cân
bởi hà trang
06/09/2017
Em hk biết bắt đầu từ đâu với bài này. Mn giúp e với ạ :(((
Chứng minh rằng trong một tam giác cân thì trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và điểm cách đều ba cạnh là bốn điểm thẳng hàng??
Theo dõi (0) 3 Trả lời
