Giải bài 79 tr 51 sách BT Toán lớp 7 Tập 2
Cho tam giác \(ABC\) có \(AB = AC = 13cm, BC = 10cm.\) Tính độ dài đường trung tuyến \(AM.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Trong một tam giác cân, đường trung tuyến ứng với cạnh đáy cũng đồng thời là đường cao của tam giác đó.
+) Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
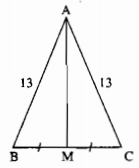
∆ABC cân tại A nên đường trung tuyến AM cũng là đường cao.
\( \Rightarrow AM \bot BC\)
\(MB = MC = {1 \over 2}BC = 5\left( {cm} \right)\)
Trong tam giác vuông AMB có \(\widehat {AMB} = 90^\circ \)
Theo định lý Pytago ta có:
\(A{B^2} = A{M^2} + M{B^2}\)
\(\eqalign{
& \Rightarrow A{M^2} = A{B^2} - M{B^2} = {15^2} - {5^2} \cr
& = 169 - 25 = 144 \Rightarrow AM = 12\left( {cm} \right) \cr} \)
-- Mod Toán 7 HỌC247
-
Chứng minh BD vuông góc AC biết đường cao CH cắt tia phân giác của góc A tại D
bởi thu hảo
25/02/2019
Cho tam giác ABC cân tại A, đường cao Ch cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC
Theo dõi (0) 1 Trả lời -
Đề thi HK2 môn Toán 7
bởi Duy Quang
05/12/2019
bạn nào thi môn toán rồi cho mình xem đề với
Theo dõi (0) 1 Trả lời -
Chứng minh BM vuông góc với FC biết tam giác ABC vuông tại A có phân giác BM
bởi thi trang
05/12/2019
Cho tam giác ABC vuông tại A, đường phân giác BM, từ M kẻ MH vuông góc với BC (H thuộc BC)
Tia BA và tia HM cắt nhau tại F. Cm : BM vuông góc với FC
Giúp mik với Mik cần rất gấp !!!!!!!!!!!!
Help me!!!!!!!!!
Theo dõi (0) 1 Trả lời -
Chứng minh BC vuông góc Ox biết D là hình chiếu của điểm A trên Oy, C là giao điểm của AD và OH
bởi thi trang
26/04/2019
Cho goc nhon xOy. Diem H nam tren tia phan giac cua goc xOy. Tu H dung cac duong vuong goc xuong 2 canh Ox va Oy (A thuoc Ox va B thuoc Oy).
a) CMR tam giác HAB cân
b) Goi D là hình chiếu của diem A trên Oy, C là giao diem của AD với OH. CM BC vuông góc Ox
c) Khi góc xOy bằng 60 dô, CM OA=2OD
Theo dõi (0) 1 Trả lời -
Chứng minh góc IAK=90 độ biết tam giác ABC có góc A nhọn, đường coa BD và CE
bởi Bin Nguyễn
26/04/2019
Cho tam giác ABC, có góc A là góc nhọn ( < 90 độ ) Vẽ đường cao BD, CE. Trên tia đối của tia BD, lấy điểm I, trên tia đối tia CE lấy điểm K sao cho BI = AC và CK = AB. Chứng minh rằng:
a) Ay = AK
b) Góc IAK = 90 độ
Theo dõi (0) 1 Trả lời -
So sánh AH và OM biết tam giác ABC có trung tuyến AM, H là trực tâm, O là giao điểm các đường trung trực
bởi Lê Tường Vy
08/05/2019
Cho tam giác nhọn ABC, trung tuyến AM. Gọi H là trực tâm, O là giao điểm của các đường trung trực của \(\Delta ABC\)
a. So sánh AH và OM
b. Gọi G là giao điểm của AM và OH. Chứng minh G là trọng tâm của ΔABC
Theo dõi (0) 1 Trả lời -
Chứng minh CB là tia phân giác của góc FCH biết tam giác ABC cân tại A có 2 đường cao BD và CE
bởi Ban Mai
08/05/2019
cho tam giác ABC cân tại A( góc A <90 độ). 2 đường cao BD và CE cắt nhau tại H .tia AH cắt BC tại I.
a) chứng minh tam giác ABD= tam giác ACE
b) chứng minh I là trung điểm của BC
c) từ C kẻ đường thẳng vuông góc với AC, cắt AH tại F. chứng minh CB là tia phân giác của góc FCH
d) giả xử góc BAC=60 độ,AB=4 cm. tính khoảng cách từ B đến CF
Theo dõi (0) 1 Trả lời -
Vì sao trực tâm của tam giác tù nằm bên ngoài tam giác ?
bởi thu thủy
17/05/2019
Hãy giải thích tại sao trực tâm của tam giác tù nằm ở bên ngoài tam giác.
giúp mk nha btập hè đó
Theo dõi (0) 1 Trả lời -
Chứng minh 3 đường thẳng BA, MD, CE cùng đi qua 1 điểm biết tam giác ABC vuông ở A có góc B=60 độ
bởi Co Nan
17/05/2019
cho tam giac ABC vuông ở A có góc B bằng 60 độ. tia phân giác của góc B cắt cạnh AC tại D. kẻ DM vuông góc BC tại M . kẻ CE vuông góc với tia BD tại E. chứng minh rằng:
a, BA=BM và BD vuông góc AM
b, MB=MC
c, ba đường thẳng BA , MD , Ce cùng đi qua một điểm
Theo dõi (0) 1 Trả lời -
Đề thi học kì 2 môn Toán 7
bởi Nguyễn Vân
19/05/2019
Bạn nào thi toán 7 -văn 7 hk2 rồi cho mk cái đề hình -toán or tập làm văn -văn nhé .Các bạn dành vài phút cho mk nhé .Mình cảm ơn nhiều ,mk sẽ tick cho bn đc nhiều đề(phải là đề thi của các bạn nhá).Mk ở Can Lộc
Mk đang cần gấp mai mk thi rùi ^^ @_@ $_$Theo dõi (0) 1 Trả lời -
Vì sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm bên ngoài tam giác ?
bởi Nguyễn Thủy
27/05/2019
HÃY GIẢI THÍCH TẠI SAO TRỰC TÂM CỦA TAM GIÁC VUÔNG TRÙNG VỚI ĐỈNH GÓC VUÔNG VÀ TRỰC TÂM CỦA TAM GIÁC TÙ NẰM Ở BÊN NGOÀI TAM GIÁC ????
GIÚP MÌNH NGAY BÂY GIỜ NHÉ!!!!!!!!!!!!!!!! MÌNH XIN CẢM ƠN!!! CỰC CỰC CỰC VÀ CỰC CỰC KÌ CẢM ƠN NHÉ!!!!!!!!!!!!!!!!!!!!!!!!!!!!11
Theo dõi (0) 1 Trả lời -
cho tm giac ABCX co cac duong cao BD va CE bang nhau chung minh rang tam giac do la 1 tam giac can
Theo dõi (0) 1 Trả lời -
Có bao nhiêu cách chứng minh 3 điểm thẳng hàng?
bởi Lê Nguyễn Hạ Anh
10/12/2019
Cho mik hỏi có bao nhiêu cách chứng minh 3 điểm thẳng hàng.Chỉ trong chương trình hk2 của lớp 7 thui nha. Mong các bạn giúp đỡ mik nha. Mai mik thi rùi. Cảm ơn trước nhá.
Theo dõi (0) 1 Trả lời -
Bài 81* trang 51 sách bài tập toán 7 tập 2
bởi hai trieu
29/09/2018
Bài 81* (Sách bài tập - tập 2 - trang 51)Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (h.17)
a) Chứng minh rằng A là trung điểm của EF
b) Các đường cao của tam giác ABC là các đường trung trục của tam giác nào ?
Theo dõi (0) 1 Trả lời -
Bài 80 trang 51 sách bài tập toán 7 tập 2
bởi Nguyễn Trà Long
29/09/2018
Bài 80 (Sách bài tập - tập 2 - trang 51)Cho tam giác ABC có góc B và góc C là các góc nhọn, AC > AB. Kẻ đường cao AH.
Chứng minh rằng :
\(\widehat{HAB}< \widehat{HAC}\)
Theo dõi (0) 1 Trả lời -
Bài 78 trang 51 sách bài tập toán 7 tập 2
bởi Mai Rừng
29/09/2018
Bài 78 (Sách bài tập - tập 2 - trang 51)Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC ?
Theo dõi (0) 1 Trả lời -
Bài 77 trang 51 sách bài tập toán 7 tập 2
bởi Nhat nheo
29/09/2018
Bài 77 (Sách bài tập - tập 2 - trang 51)Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của tam giác ABC, đường cao AF của tam giác ACD.
Chứng minh rằng :
\(\widehat{EAF}=90^0\)
Theo dõi (0) 1 Trả lời -
Bài 76 trang 51 sách bài tập toán 7 tập 2
bởi con cai
29/09/2018
Bài 76 (Sách bài tập - tập 2 - trang 51)Cho tam giác ABC cân tại A, đường trung tuyến AM. Qua A kẻ đường thẳng d vuông góc với AM. Chứng minh rằng d song song với BC ?
Theo dõi (0) 1 Trả lời -
Bài 73 trang 51 sách bài tập toán 7 tập 2
bởi Trieu Tien
29/09/2018
Bài 73 (Sách bài tập - tập 2 - trang 51)Tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng tam giác đó cân ?
Theo dõi (0) 1 Trả lời -
Bài 72 trang 51 sách bài tập toán 7 tập 2
bởi Nguyễn Thị Thanh
29/09/2018
Bài 72 (Sách bài tập - tập 2 - trang 51)
Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HAB, HAC, HBC ?
Theo dõi (0) 1 Trả lời -
Chứng minh tam giác ABC có các đường cao BD và CE bằng nhau là tam giác cân
bởi Nguyễn Minh Minh
11/12/2019
cho tam giác ABC có các đường cao BD và CE bằng nhau chứng minh rằng tam giác đó là 1 tam giác cân
các pn giúp mink nha (mai mink học rồi)
Theo dõi (0) 1 Trả lời -
Cho hình 57
a) C/m NS vuông góc với LM
b) Khi góc LNP = 50 độ , hãy tính góc MSP và góc PSQ.
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC vuông tại A,đường cao AH .trên cạnh BC lấy điểm D sao cho BD=AB.
a,CMR góc BAH=HCA
b,Vẽ DK vuông góc AC(K thuộc AC).CMR AK=AH
c,Tia KD cắt tia AH tại E .CMR AD vuông goc CE
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC cân tại A <90o.Kẻ BH vuông góc với AC,CK vuông góc với AB(H thuộc BC,K thuộc AB).Gọi O là giao điểm của BH và CK
a)chứng minh tam giác ABH=tam giác ACK
b)chứng minh tam giác OBK=tam giác OCH
c)trên nữa mặt phẳng bờ BC không chứa điểm A lấy điểm I sao cho IB=IC.chứng minh ba điểm A,O,I thẳng hàng
Theo dõi (0) 1 Trả lời
