Phần hướng dẫn giải bài tập SGK Hình học 7 Chương 3 Bài 9 Tính chất ba đường cao của tam giác - Luyện tập sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 7 Tập hai.
-
Bài tập 58 trang 83 SGK Toán 7 Tập 2
Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm tâm của tam giác tù nằm ở bên ngoài tam giác
-
Bài tập 59 trang 83 SGK Toán 7 Tập 2
Cho hình 57.
a) Chứng minh \(N{\rm{S}} \bot LM\)
b) Khi \(\widehat {LNP} = {50^o}\), hãy tính góc MSP và góc PSQ
-
Bài tập 60 trang 83 SGK Toán 7 Tập 2
Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng l vuông góc với d tại J. Trên l lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.
Chứng minh rằng \(KN \bot IM\)
-
Bài tập 61 trang 83 SGK Toán 7 Tập 2
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của tam giác HAB và HAC.
-
Bài tập 62 trang 83 SGK Toán 7 Tập 2
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
-
Bài tập 70 trang 50 SBT Toán 7 Tập 2
Cho tam giác \(ABC\) vuông tại \(B.\) Điểm nào là trực tâm của tam giác đó?
-
Bài tập 71 trang 50 SBT Toán 7 Tập 2
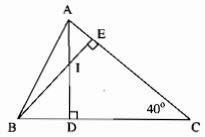
Cho hình 15.
a) Chứng minh rằng: \(CI \bot AB.\)
b) Cho \(\widehat {ACB} = 40^\circ \). Tính \(\widehat {BI{\rm{D}}},\widehat {DIE}\)
-
Bài tập 72 trang 51 SBT Toán 7 Tập 2
Cho \(H\) là trực tâm của tam giác \(ABC\) không vuông. Tìm trực tâm của các tam giác \(HAB, HAC, HBC.\)
-
Bài tập 73 trang 51 SBT Toán 7 Tập 2
Tam giác \(ABC\) có các đường cao \(BD\) và \(CE\) bằng nhau. Chứng minh rằng tam giác đó là tam giác cân.
-
Bài tập 74 trang 51 SBT Toán 7 Tập 2
Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Tìm trực tâm của tam giác \(ABC, AHB, AHC.\)
-
Bài tập 75 trang 51 SBT Toán 7 Tập 2
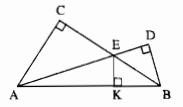
Cho hình 16. Có thể khẳng định rằng các đường thẳng \(AC, BD, KE\) cùng đi qua một điểm hay không? Vì sao?
-
Bài tập 76 trang 51 SBT Toán 7 Tập 2
Cho tam giác \(ABC\) cân tại \(A,\) đường trung tuyến \(AM.\) Qua \(A\) kẻ đường thẳng \(d\) vuông góc với \(AM.\) Chứng minh rằng \(d\) song song với \(BC.\)
-
Bài tập 77 trang 51 SBT Toán 7 Tập 2
Cho tam giác \(ABC \) cân tại \(A.\) Vẽ điểm \(D\) sao cho \(A\) là trung điểm của \(BD.\) Kẻ đường cao \(AE\) của \(∆ABC,\) đường cao \(AF\) của \(∆ACD.\) Chứng minh rằng \(\widehat {EAF} = 90^\circ \)
-
Bài tập 78 trang 51 SBT Toán 7 Tập 2
Cho tam giác \(ABC\) cân tại \(A,\) đường cao \(CH\) cắt tia phân giác của góc \(A\) tại \(D.\) Chứng minh rằng \(BD\) vuông góc với \(AC.\)
-
Bài tập 79 trang 51 SBT Toán 7 Tập 2
Cho tam giác \(ABC\) có \(AB = AC = 13cm, BC = 10cm.\) Tính độ dài đường trung tuyến \(AM.\)
-
Bài tập 80 trang 51 SBT Toán 7 Tập 2
Cho tam giác \(ABC\) có \(\widehat B,\widehat C\) là các góc nhọn, \(AC > AB.\) Kẻ đường cao \(AH.\) Chứng minh rằng \(\widehat {HAB} < \widehat {HAC}.\)
-
Bài tập 81 trang 51 SBT Toán 7 Tập 2
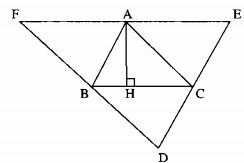
Cho tam giác \(ABC.\) Qua mỗi đỉnh \(A, B, C\) kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác \(DEF\) (h.17)
a) Chứng minh rằng \(A\) là trung điểm \(EF.\)
b) Các đường cao của tam giác \(ABC\) là các đường trung trực của tam giác nào?

.PNG)





