Bài tập 3 trang 39 SGK Hình học 12

Câu a:

Đường sinh l của hình nón là:

l = \(\small 5\sqrt{41}\) (cm).

Diện tích xung quanh của hình nón là:

Sxq = πrl = 125π√41 (cm²)

Câu b:

V_nón = (625.20π)/3 = (12500π)/3 (cm³)

Câu c:

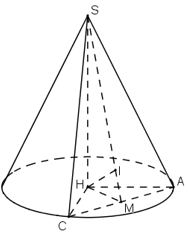
Gọi hình nón đã cho có đỉnh là S và H là tâm đường tròn đáy.

Thiết diện đi qua đỉnh S là tam giác SAC (với A và C thuộc đường tròn đáy)

Gọi M là trung điểm của AC.

Ta có: \(\left\{ \begin{array}{l}
AC \bot HM\\
AC \bot SH
\end{array} \right. \Rightarrow AC \bot mp\left( {SHM} \right)\)

\( \Rightarrow \left( {SAC} \right) \bot \left( {SHM} \right)\) theo giao tuyến SM

Trong mp(SHM) kẻ \(HI \bot SM \Rightarrow HI \bot \left( {SAC} \right)\)

Do đó, d( H; (SAC))= HI = 12

Trong tam giác vuông SHM ta có:

\(\begin{array}{l}
\frac{1}{{H{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{M^2}}} \Rightarrow \frac{1}{{H{M^2}}} = \frac{1}{{H{I^2}}} - \frac{1}{{S{H^2}}}\\
 \Rightarrow \frac{1}{{H{M^2}}} = \frac{1}{{{{12}^2}}} - \frac{1}{{{{20}^2}}} = \frac{1}{{225}} \Rightarrow HM = 15
\end{array}\)

Trong tam giác vuông HAM ta có:

\(A{M^2} = H{A^2} - H{M^2} = {25^2} - {15^2} = 400\) nên AM = 20(cm)

Ta có:

\(\begin{array}{l}
\sin \widehat {HSM} = \frac{{HM}}{{SM}} = \frac{{HI}}{{SH}}\\
 \Rightarrow SM = \frac{{HM.SH}}{{HI}} = \frac{{15.20}}{{12}} = 25
\end{array}\)

Do đó, diện tích thiết diện SAC là:

\(\begin{array}{l}
{S_{SAC}} = \frac{1}{2}.AC.SM = AM.SM\\
 = 20.25 = 500\left( {c{m^2}} \right)
\end{array}\)

-- Mod Toán 12 HỌC247