Giải bài 7 tr 39 sách GK Toán Hình lớp 12
Một hình trụ có bán kính r và chiều cao \(h = r \sqrt {3}\).
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.
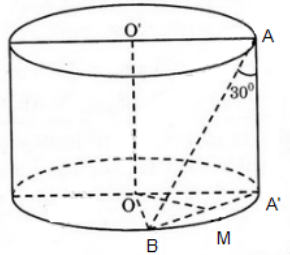
c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Hướng dẫn giải chi tiết bài 7
Câu a:
Theo công thức ta có:
\(\small S_{xq} = 2\pi.r.h = 2\sqrt{3} \pi.r^2\)
\({S_t}_p = 2\pi .r.h + 2\pi .{r^2} = 2\sqrt 3 \pi .{r^2} + 2\pi .{r^2} = 2(\sqrt 3 + 1)\pi .{r^2}\) ( đơn vị thể tích)
Câu b:
\(\small V_{{tru}} = \pi.R^2.h = \sqrt{3} \pi r^3\)
Câu c:
Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm của AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có J1 là trung điểm của AB1, O1J1 = IJ.
Theo giả thiết \(\widehat {{B_1}BA}\) = 300.
do vậy: AB1 = BB1.tan 300 = \(\frac{{\sqrt 3 }}{3}h\) = r.
Xét tam giác vuông O1J1A vuông tại J1, ta có: \({O_1}{J_1}^2 = {O_1}{A^2} - A{J_1}^2 = {r^2} - \frac{{{r^2}}}{2} = \frac{3}{4}{r^2}\)
Vậy khoảng cách giữa AB và O1O2 : \(\frac{{\sqrt 3 }}{2}r\)
-- Mod Toán 12 HỌC247
-


Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\). Cho hai điểm \(A\) và \(B\) lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng \(AB\) và trục của hình trụ bằng \(30^0\). Tính khoảng cách giữa đường thẳng \(AB\) và trục của hình trụ.
bởi Nguyễn Hồng Tiến
 05/06/2021
05/06/2021
Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\). Cho hai điểm \(A\) và \(B\) lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng \(AB\) và trục của hình trụ bằng \(30^0\). Tính khoảng cách giữa đường thẳng \(AB\) và trục của hình trụ.
Theo dõi (0) 1 Trả lời -


Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\). Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.
bởi Trần Thị Trang
 06/06/2021
06/06/2021
Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\). Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.
Theo dõi (0) 1 Trả lời -


Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\). Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
bởi Anh Linh
 06/06/2021
06/06/2021
Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\). Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 5 trang 39 SGK Hình học 12
Bài tập 6 trang 39 SGK Hình học 12
Bài tập 8 trang 40 SGK Hình học 12
Bài tập 9 trang 40 SGK Hình học 12
Bài tập 10 trang 40 SGK Hình học 12
Bài tập 2.1 trang 46 SBT Hình học 12
Bài tập 2.2 trang 47 SBT Hình học 12
Bài tập 2.3 trang 47 SBT Hình học 12
Bài tập 2.4 trang 47 SBT Hình học 12
Bài tập 2.5 trang 47 SBT Hình học 12
Bài tập 2.6 trang 47 SBT Hình học 12
Bài tập 2.7 trang 47 SBT Hình học 12
Bài tập 2.8 tr 47 SBT Hình học 12
Bài tập 2.9 trang 47 SBT Hình học 12
Bài tập 2.10 trang 48 SBT Hình học 12
Bài tập 2.11 trang 48 SBT Hình học 12
Bài tập 2.12 trang 49 SBT Hình học 12
Bài tập 11 trang 53 SGK Hình học 12 NC
Bài tập 12 trang 53 SGK Hình học 12 NC
Bài tập 13 trang 53 SGK Hình học 12 NC
Bài tập 14 trang 53 SGK Hình học 12 NC
Bài tập 15 trang 53 SGK Hình học 12 NC
Bài tập 16 trang 54 SGK Hình học 12 NC
Bài tập 17 trang 59 SGK Hình học 12 NC
Bài tập 18 trang 59 SGK Hình học 12 NC
Bài tập 19 trang 60 SGK Hình học 12 NC





