Giải bài 4.19 tr 165 SBT Toán 11
Cho hàm số \(f(x) = \left\{ \begin{array}{l}
{x^2},\,\,\,\,\,\,\,\,\,x \ge 0\\
{x^2} - 1,\,\,x < 0
\end{array} \right.\)
a) Vẽ đồ thị của hàm số Từ đó dự đoán về giới hạn của khi x → 0
b) Dùng định nghĩa chứng minh dự đoán trên.
Hướng dẫn giải chi tiết
a) \(f(x) = \left\{ \begin{array}{l}
{x^2},\,\,\,\,\,\,\,\,\,x \ge 0\\
{x^2} - 1,\,\,x < 0
\end{array} \right.\)
Tập xác đinh
+) Vẽ parabol y . Xóa phần đồ thị của hàm số trên nửa mặt phẳng bờ là Oy.
+ Vẽ parabol . Xóa phần đồ thị của hàm số trên nửa mặt phẳng bờ là Oy.
Ta được đồ thị của hàm số
Từ đồ thị hàm số f(x) dự đoán: Hàm số f(x) không có giới hạn khi x → 0
b) Lấy hai dãy số có số hạng tổng quát là \({a_n} = \frac{1}{n}\) và \({b_n} = - \frac{1}{n}\)
Ta có, \({a_n} \to 0\) và \({b_n} \to 0\) khi \(n \to + \infty \)
Vì \(\frac{1}{n} > 0\) nên \(f\left( {{a_n}} \right) = \frac{1}{{{n^2}}}\)
Do đó \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{a_n}} \right) = \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^2}}} = 0\)
Vì \( - \frac{1}{n} \le 0\) nên \(f\left( {{b_n}} \right) = \frac{1}{{{n^2}}} - 1\)
Do đó \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{b_n}} \right) = \mathop {\lim }\limits_{n \to + \infty } \left( {\frac{1}{{{n^2}}} - 1} \right) = - 1\)
Do vậy không có giới hạn khi x →o 0.
-- Mod Toán 11 HỌC247
-


Cho hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cùng xác định trên khoảng \(\left( { - \infty ,a} \right)\). Dùng định nghĩa chứng minh rằng, nếu \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L\) và \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = M\) thì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right).g\left( x \right) = L.M\).
bởi sap sua
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Chứng minh rằng hàm số \(y = \sin x\) không có giới hạn khi \(x \to + \infty \).
bởi Lê Tấn Thanh
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Dùng định nghĩa tìm giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {{{x^3} + 1} \over {{x^2} + 1}}\)
bởi Nguyen Nhan
 28/02/2021
Theo dõi (0) 1 Trả lời
28/02/2021
Theo dõi (0) 1 Trả lời -


Dùng định nghĩa tìm giới hạn: \(\mathop {\lim }\limits_{x \to 5} {{x + 3} \over {3-x}}\).
bởi Ngoc Nga
 28/02/2021
Theo dõi (0) 1 Trả lời
28/02/2021
Theo dõi (0) 1 Trả lời -


Tinh giới hạn của các hàm số sau
bởi Lê Duy
 28/02/2021
28/02/2021
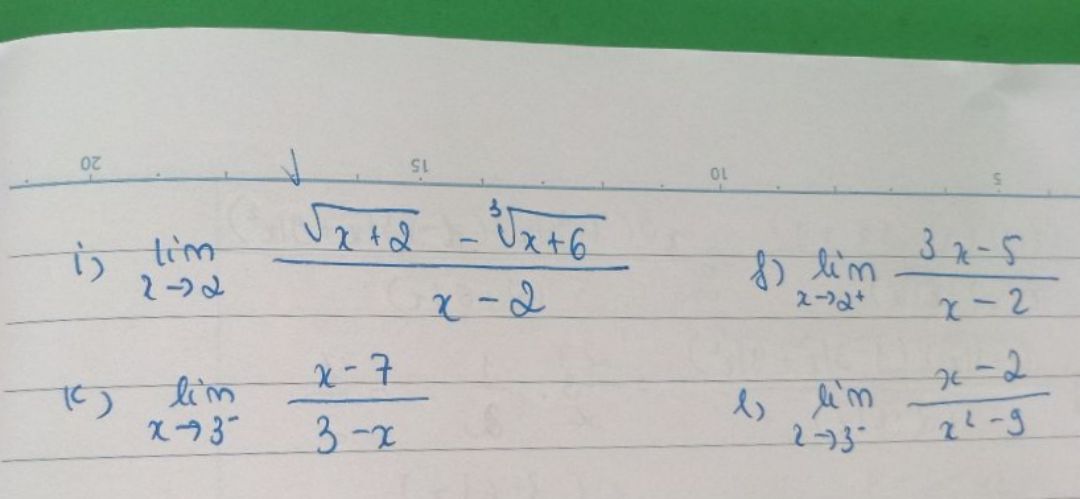 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính: \(\eqalign{&\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} + 1} + x} \over {5 - 2x}} \cr} \)
bởi Nhi Nhi
 23/02/2021
Theo dõi (0) 1 Trả lời
23/02/2021
Theo dõi (0) 1 Trả lời -


Tính: \(\eqalign{&\mathop {\lim }\limits_{x \to - \infty } (\sqrt {{x^2} - 2x + 5}) \cr } \)
bởi Anh Trần
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 133 SGK Đại số & Giải tích 11
Bài tập 4.18 trang 165 SBT Toán 11
Bài tập 4.20 trang 165 SBT Toán 11
Bài tập 4.21 trang 165 SBT Toán 11
Bài tập 4.22 trang 165 SBT Toán 11
Bài tập 4.23 trang 165 SBT Toán 11
Bài tập 4.24 trang 165 SBT Toán 11
Bài tập 4.25 trang 166 SBT Toán 11
Bài tập 4.26 trang 166 SBT Toán 11
Bài tập 4.27 trang 166 SBT Toán 11
Bài tập 4.28 trang 166 SBT Toán 11
Bài tập 4.29 trang 166 SBT Toán 11
Bài tập 4.30 trang 166 SBT Toán 11
Bài tập 4.31 trang 167 SBT Toán 11
Bài tập 21 trang 151 SGK Toán 11 NC
Bài tập 22 trang 152 SGK Toán 11 NC
Bài tập 23 trang 152 SGK Toán 11 NC
Bài tập 24 trang 152 SGK Toán 11 NC
Bài tập 25 trang 152 SGK Toán 11 NC
Bài tập 26 trang 158 SGK Toán 11 NC
Bài tập 27 trang 158 SGK Toán 11 NC
Bài tập 28 trang 158 SGK Toán 11 NC
Bài tập 29 trang 159 SGK Toán 11 NC
Bài tập 30 trang 159 SGK Toán 11 NC
Bài tập 31 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC





