Giải bài 4.24 tr 165 SBT Toán 11
Tính giới hạn của các hàm số sau khi \(x \to - \infty \) và \(x \to + \infty \)
a) \(f\left( x \right) = \frac{{\sqrt {{x^2} - 3x} }}{{x + 2}}\);
b) \(f(x) = x + \sqrt {{x^2} - x + 1} ;\)
c)
Hướng dẫn giải chi tiết
a) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} - 3x} }}{{x + 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {1 - \frac{3}{x}} }}{{x\left( {1 + \frac{2}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {1 - \frac{3}{x}} }}{{1 + \frac{2}{x}}} = - 1\)
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} - 3x} }}{{x + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt {1 - \frac{3}{x}} }}{{x\left( {1 + \frac{2}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 - \frac{3}{x}} }}{{1 + \frac{2}{x}}} = 1\)
b)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} - x + 1} } \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 1}}{{x - \sqrt {{x^2} - x + 1} }}\\
= \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {1 - \frac{1}{x}} \right)}}{{x\left( {1 + \sqrt {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} } \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{1 - \frac{1}{x}}}{{1 + \sqrt {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} }} = \frac{1}{2}
\end{array}\)
\(\mathop {\lim }\limits_{x \to + \infty } \left( {x + \sqrt {{x^2} - x + 1} } \right) = \mathop {\lim }\limits_{x \to + \infty } x\left( {1 + \sqrt {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} } \right) = + \infty \)
c)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - x} - \sqrt {{x^2} + 1} } \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x - 1}}{{\sqrt {{x^2} - x} + \sqrt {{x^2} + 1} }}\\
= \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( { - 1 - \frac{1}{x}} \right)}}{{ - x\left( {\sqrt {1 - \frac{1}{x}} + \sqrt {1 + \frac{1}{x}} } \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1 - \frac{1}{x}}}{{ - \left( {\sqrt {1 - \frac{1}{x}} + \sqrt {1 + \frac{1}{x}} } \right)}} = \frac{1}{2}
\end{array}\)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - x} - \sqrt {{x^2} + 1} } \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - x - 1}}{{\sqrt {{x^2} - x} + \sqrt {{x^2} + 1} }}\\
= \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( { - 1 - \frac{1}{x}} \right)}}{{x\left( {\sqrt {1 - \frac{1}{x}} + \sqrt {1 + \frac{1}{x}} } \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1 - \frac{1}{x}}}{{\sqrt {1 - \frac{1}{x}} + \sqrt {1 + \frac{1}{x}} }} = - \frac{1}{2}
\end{array}\)
-- Mod Toán 11 HỌC247
-


Tính giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{{x^2} + 3x - 4}}{{x - 2}}\)?
bởi Phạm Khiêm
 07/06/2020
07/06/2020
Làm câu 1
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left( {x + 2} \right)\sqrt {\frac{{x - 1}}{{{x^3} + x}}} \)?
bởi Nguyễn Thị MỹÝ
 07/06/2020
07/06/2020
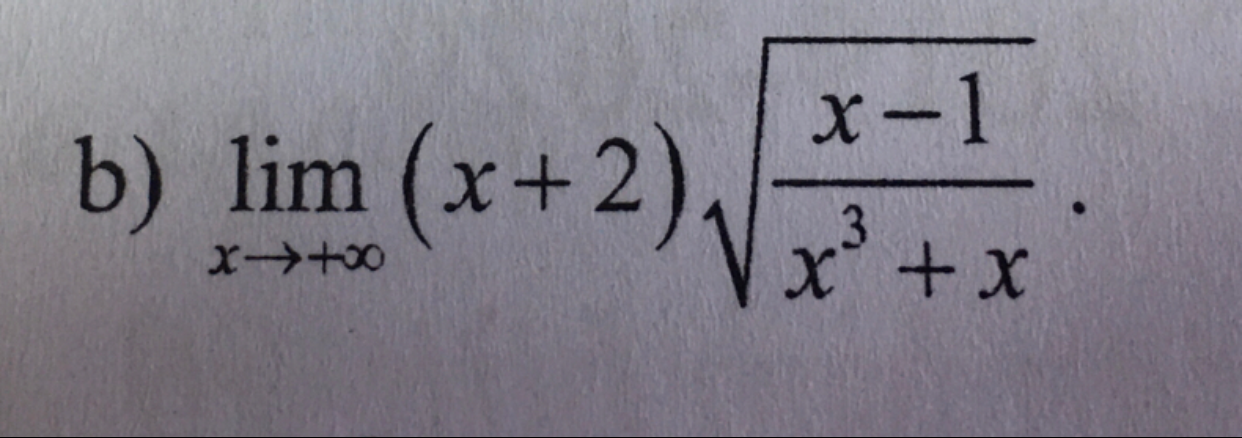 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tính tổng a+2b?
bởi Tran Thi Phuong
 05/06/2020
05/06/2020
Giúp e giải chi tiết với ạ
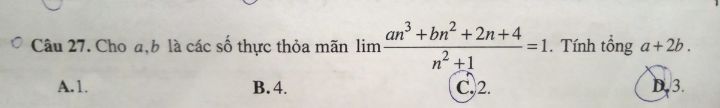 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính (mathop {lim }limits_{x o infty } frac{{2x - sqrt {{x^2} + 8x} }}{{x + 3}})
bởi Như Huyền
 04/06/2020
04/06/2020
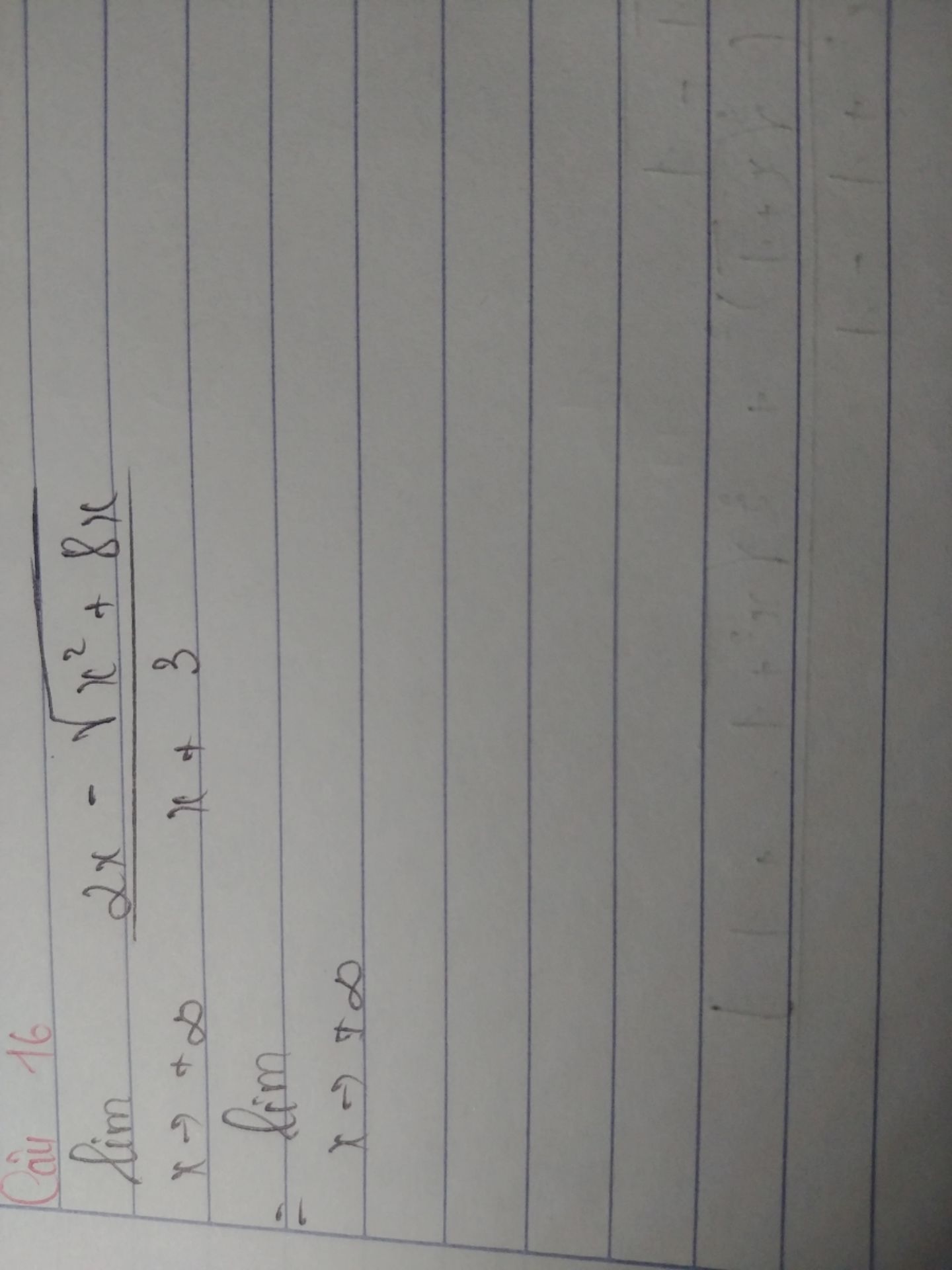 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính tổng a+2b?
bởi Tran Thi Phuong
 01/06/2020
01/06/2020
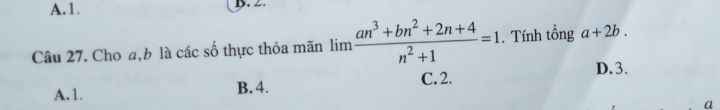 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Trong các khẳng định sau, khẳng định nào sai?
bởi Lê Bảo An
 30/05/2020
30/05/2020
A. Một dãy số là một hàm số.
B. Dãy số \({u_n} = {\left( { - \frac{1}{2}} \right)^{n - 1}}\) là dãy số không tăng cũng không giảm dưới.
C. Mỗi dãy số tăng là một dãy số bị chặn.
D. Một hàm số là một dãy số.
Theo dõi (0) 3 Trả lời -

 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 4.22 trang 165 SBT Toán 11
Bài tập 4.23 trang 165 SBT Toán 11
Bài tập 4.25 trang 166 SBT Toán 11
Bài tập 4.26 trang 166 SBT Toán 11
Bài tập 4.27 trang 166 SBT Toán 11
Bài tập 4.28 trang 166 SBT Toán 11
Bài tập 4.29 trang 166 SBT Toán 11
Bài tập 4.30 trang 166 SBT Toán 11
Bài tập 4.31 trang 167 SBT Toán 11
Bài tập 21 trang 151 SGK Toán 11 NC
Bài tập 22 trang 152 SGK Toán 11 NC
Bài tập 23 trang 152 SGK Toán 11 NC
Bài tập 24 trang 152 SGK Toán 11 NC
Bài tập 25 trang 152 SGK Toán 11 NC
Bài tập 26 trang 158 SGK Toán 11 NC
Bài tập 27 trang 158 SGK Toán 11 NC
Bài tập 28 trang 158 SGK Toán 11 NC
Bài tập 29 trang 159 SGK Toán 11 NC
Bài tập 30 trang 159 SGK Toán 11 NC
Bài tập 31 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC





