Giải bài 4.22 tr 165 SBT Toán 11
Tìm giới hạn của các hàm số sau
a) \(f(x) = \frac{{{x^2} - 2x - 3}}{{x - 1}}\) khi \(x\to 3\)
b) \(h(x) = \frac{{2{x^3} + 15}}{{{{(x + 2)}^2}}}\) khi \(x\to -2\)
c) \(k(x) = \sqrt {4{x^2} - x + 1} \) khi \(x \to - \infty \)
d) \(h(x) = \frac{{x - 15}}{{x + 2}}\) khi \(x \to - {2^ + }\) và
Hướng dẫn giải chi tiết
a) \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 2x - 3}}{{x - 1}} = \frac{{{3^2} - 2.3 - 3}}{{3 - 1}} = 0\)
b) \(\mathop {\lim }\limits_{x \to - 2} h\left( x \right) = \mathop {\lim }\limits_{x \to - 2} \frac{{2{x^3} + 15}}{{{{\left( {x + 2} \right)}^2}}} = - \infty \)
Vì \(\mathop {\lim }\limits_{x \to - 2} \left( {2{x^3} + 15} \right) = - 1 < 0\) và \(\mathop {\lim }\limits_{x \to - 3} {\left( {x + 2} \right)^2} = 0\)
c)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } k\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \sqrt {4{x^2} - x + 1} \\
= \mathop {\lim }\limits_{x \to - \infty } \sqrt {{x^2}\left( {4 - \frac{1}{x} + \frac{1}{{{x^2}}}} \right)} \\
= \mathop {\lim }\limits_{x \to - \infty } \left| x \right|\sqrt {4 - \frac{1}{x} + \frac{1}{{{x^2}}}} = + \infty
\end{array}\)
d) \(\mathop {\lim }\limits_{x \to - {2^ + }} h\left( x \right) = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{x - 15}}{{x + 2}} = - \infty \)
Vì \(\mathop {\lim }\limits_{x \to - {2^ + }} (x - 15) = - 17 < 0\) và \(\mathop {\lim }\limits_{x \to - {2^ + }} \left( {x + 2} \right) = 0,x + 2 > 0,\forall x > - 2\)
\(\mathop {\lim }\limits_{x \to - {2^ + }} \left( {x + 2} \right) = 0,\mathop {\lim }\limits_{x \to - {2^ - }} h\left( x \right) = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{x - 15}}{{x + 2}} = + \infty ,x + 2 > 0,\forall x > - 2\)
Vì \(\mathop {\lim }\limits_{x \to - {2^ - }} (x - 15) = - 17 < 0\) và \(\mathop {\lim }\limits_{x \to - {2^ - }} \left( {x + 2} \right) = 0,x + 2 < 0,\forall x < - 2\)
-- Mod Toán 11 HỌC247
-


Trong biểu thức (1) xác định hàm số y = f(x) ở Ví dụ 4, cần thay 2 bằng số nào để hàm số có giới hạn là -2 khi x → 1?
bởi thuy tien
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời -


.png)
Quan sát đồ thị và cho biết:
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
Theo dõi (0) 1 Trả lời -


Tính limx đến 0(e^x-cosx)/sinx.
bởi Phương Nam
 19/02/2021
19/02/2021
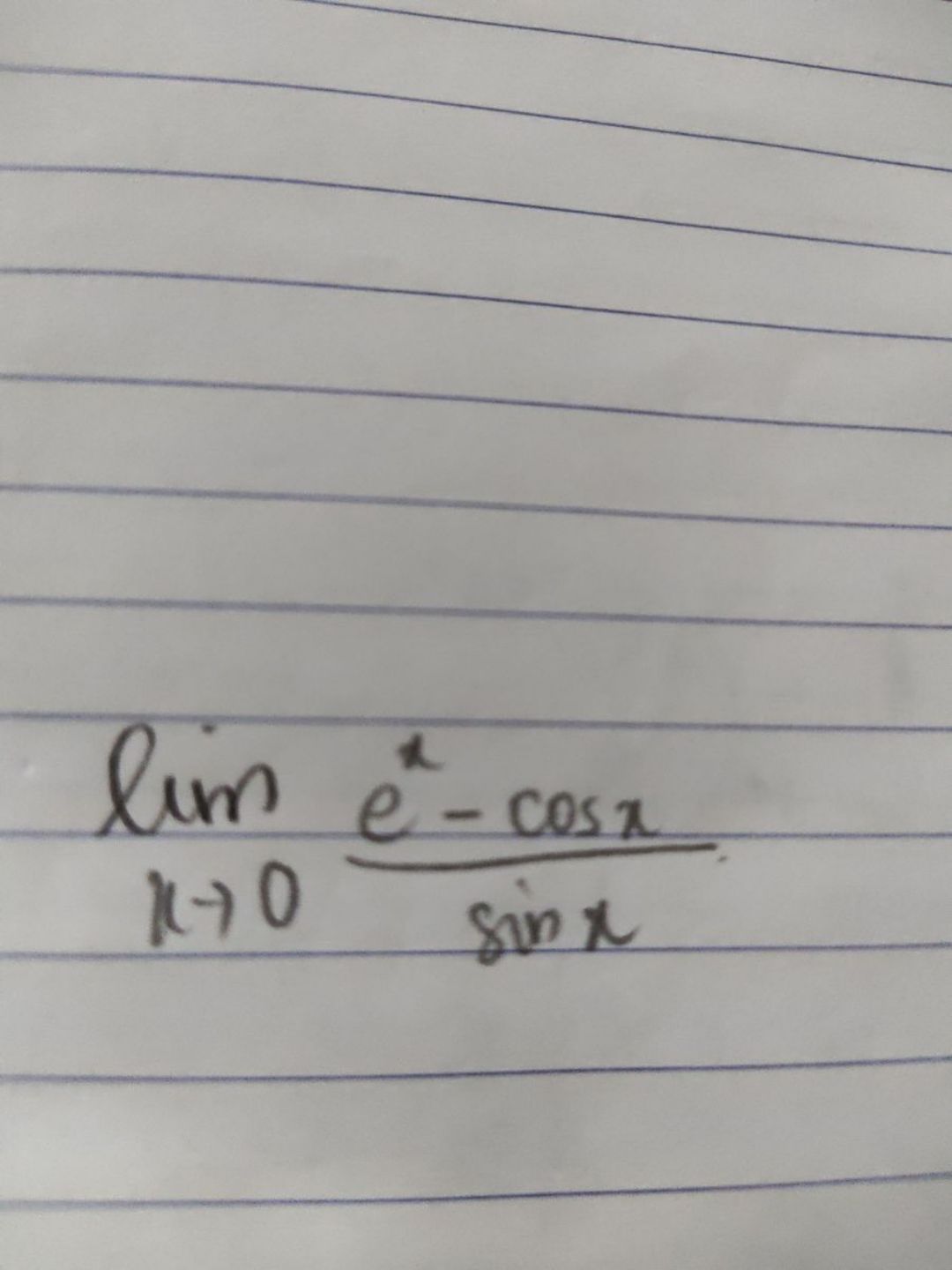 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính giới hạn
bởi Bich Hong Nguyen
 03/02/2021
03/02/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính giới hạn: lim x+ căn (x^2 +x +1) x đến âm cực
bởi Hùng Đức
 25/01/2021
25/01/2021
- lim x+ căn (x^2 +x +1) x đến âm cực
Theo dõi (0) 0 Trả lời -


Tính giới hạn của hàm số sau
bởi Kim Thủy
 25/01/2021
25/01/2021
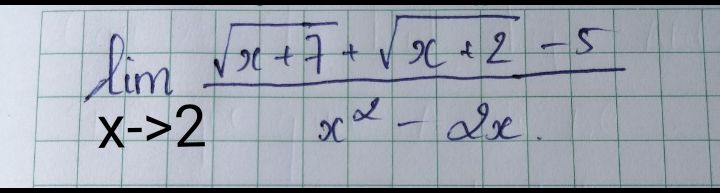 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính giới hạn của hàm số
bởi Lê Hoàng
 21/01/2021
21/01/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 4.20 trang 165 SBT Toán 11
Bài tập 4.21 trang 165 SBT Toán 11
Bài tập 4.23 trang 165 SBT Toán 11
Bài tập 4.24 trang 165 SBT Toán 11
Bài tập 4.25 trang 166 SBT Toán 11
Bài tập 4.26 trang 166 SBT Toán 11
Bài tập 4.27 trang 166 SBT Toán 11
Bài tập 4.28 trang 166 SBT Toán 11
Bài tập 4.29 trang 166 SBT Toán 11
Bài tập 4.30 trang 166 SBT Toán 11
Bài tập 4.31 trang 167 SBT Toán 11
Bài tập 21 trang 151 SGK Toán 11 NC
Bài tập 22 trang 152 SGK Toán 11 NC
Bài tập 23 trang 152 SGK Toán 11 NC
Bài tập 24 trang 152 SGK Toán 11 NC
Bài tập 25 trang 152 SGK Toán 11 NC
Bài tập 26 trang 158 SGK Toán 11 NC
Bài tập 27 trang 158 SGK Toán 11 NC
Bài tập 28 trang 158 SGK Toán 11 NC
Bài tập 29 trang 159 SGK Toán 11 NC
Bài tập 30 trang 159 SGK Toán 11 NC
Bài tập 31 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC






