Bài tập 33 trang 159 SGK Toán 11 NC
Cho hàm số
\(f\left( x \right) = \left\{ \begin{array}{l}
{x^2} - 2x + 3,\,\,\,x \le 2\\
4x - 3,\,\,\,\,\,\,\,\,\,\,\,\,\,x > 2
\end{array} \right.\)
Tìm \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\) (nếu có)
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {4x - 3} \right)\\
= 4.2 - 3 = 5
\end{array}\\
\begin{array}{l}
\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {{x^2} - 2x + 3} \right)\\
= {2^2} - 2.2 + 3 = 3
\end{array}
\end{array}\)
Vì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\).
-- Mod Toán 11 HỌC247
-


Tính lim (1^3+2^3+...+n^3)/(n^4+2n^2+5)
bởi Ly Trần Hải
 15/02/2020
Làm sao rút gọn đc như vậy ạ
15/02/2020
Làm sao rút gọn đc như vậy ạ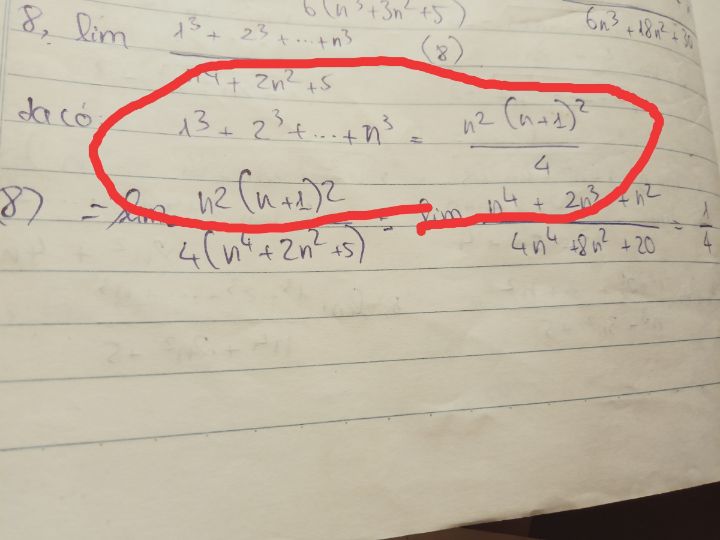 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính lim (3x^2+7x+11) khi x tiến tới 2
bởi Thủy Em
 15/02/2020
Giúp e vs
15/02/2020
Giúp e vs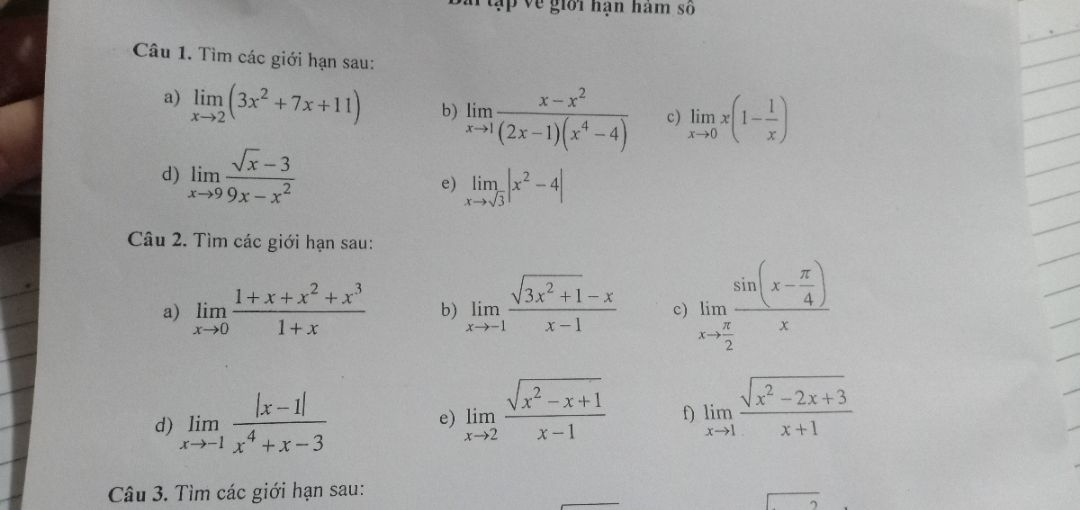 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính lim (căn(3x^2-2x+17)+căn bậc 3(3x^3-19x^2-23x-19))/(3x^2-12x+12) khi x tiến tới 2
bởi Nguyễn Hoàng
 15/02/2020
15/02/2020

mọi người làm giúp mình câu 28
Theo dõi (1) 5 Trả lời -


Tính lim (3n^2-n+1)/(n^3+4n^2+6)
bởi Ngân Hà
 14/02/2020
14/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính lim (3x-7)/(x+2) khi x tiến tới (-2)+
bởi Vy Lê Thảo
 13/02/2020
13/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Kết quả của giới hạn lim (x-15)/(x-2) khi x tiến tới 2 là?
bởi Ziii
 13/02/2020
13/02/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính lim (x+1)/(3x-2) khi x tiến tới 4
bởi Văn Dủ
 12/02/2020
Không biết giải
12/02/2020
Không biết giải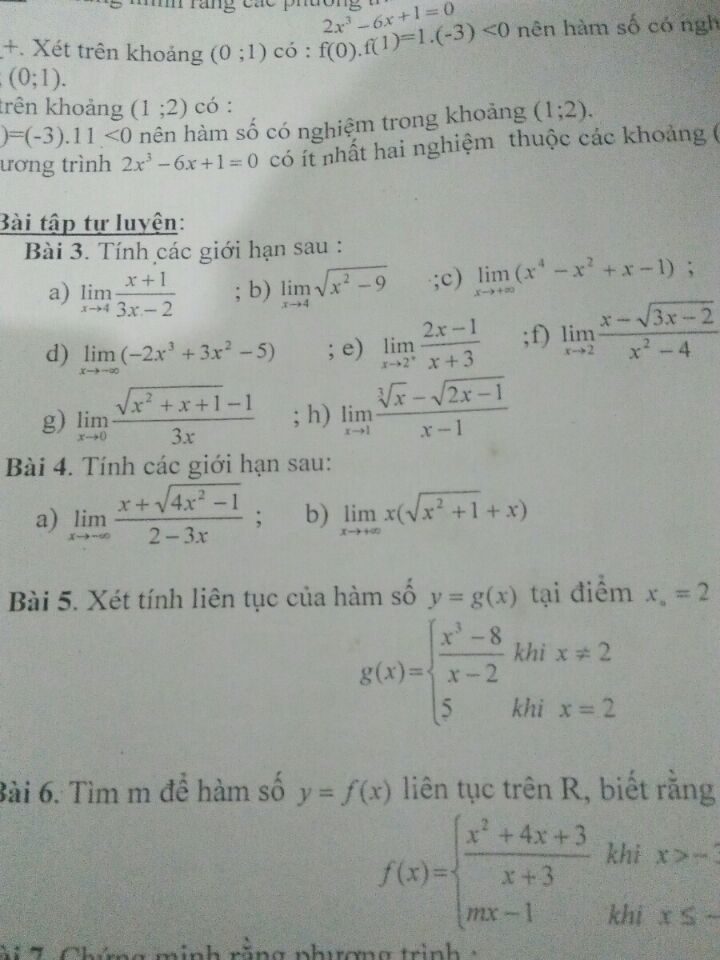 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 31 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC





