Bài tập 31 trang 159 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - \sqrt 2 } \frac{{{x^3} + 2\sqrt 2 }}{{{x^2} - 2}}\)
b) \(\mathop {\lim }\limits_{x \to 3} \frac{{{x^4} - 27x}}{{2{x^2} - 3x - 9}}\)
c) \(\mathop {\lim }\limits_{x \to - 2} \frac{{{x^4} - 16}}{{{x^2} + 6x + 8}}\)
d) \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{\sqrt {1 - x} + x - 1}}{{\sqrt {{x^2} - {x^3}} }}\)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \sqrt 2 } \frac{{{x^3} + 2\sqrt 2 }}{{{x^2} - 2}} = \mathop {\lim }\limits_{x \to - \sqrt 2 } \frac{{{x^3} + {{\left( {\sqrt 2 } \right)}^3}}}{{{x^2} - {{\left( {\sqrt 2 } \right)}^2}}}\\
= \mathop {\lim }\limits_{x \to - \sqrt 2 } \frac{{\left( {x + \sqrt 2 } \right)\left( {{x^2} - x\sqrt 2 + 2} \right)}}{{\left( {x + \sqrt 2 } \right)\left( {x - \sqrt 2 } \right)}}\\
= \mathop {\lim }\limits_{x \to - \sqrt 2 } \frac{{{x^2} - x\sqrt 2 + 2}}{{x - \sqrt 2 }} = \frac{{ - 3\sqrt 2 }}{2}
\end{array}\)
b)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\mathop {\lim }\limits_{x \to 3} \frac{{{x^4} - 27x}}{{2{x^2} - 3x - 9}}\\
= \mathop {\lim }\limits_{x \to 3} \frac{{x\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right)}}{{\left( {x - 3} \right)\left( {2x + 3} \right)}}
\end{array}\\
{ = \mathop {\lim }\limits_{x \to 3} \frac{{x\left( {{x^2} + 3x + 9} \right)}}{{2x + 3}} = 9}
\end{array}\)
c)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - 2} \frac{{{x^4} - 16}}{{{x^2} + 6x + 8}}\\
= \mathop {\lim }\limits_{x \to - 2} \frac{{\left( {{x^2} + 4} \right)\left( {{x^2} - 4} \right)}}{{\left( {x + 2} \right)\left( {x + 4} \right)}}\\
= \mathop {\lim }\limits_{x \to - 2} \frac{{\left( {{x^2} + 4} \right)\left( {x - 2} \right)}}{{x + 4}} = - 16
\end{array}\)
d)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\mathop {\lim }\limits_{x \to {1^ - }} \frac{{\sqrt {1 - x} + x - 1}}{{\sqrt {{x^2} - {x^3}} }}\\
= \mathop {\lim }\limits_{x \to {1^ - }} \frac{{\sqrt {1 - x} - \left( {1 - x} \right)}}{{\left| x \right|\sqrt {1 - x} }}
\end{array}\\
{ = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{1 - \sqrt {1 - x} }}{{\left| x \right|}} = 1}
\end{array}\)
-- Mod Toán 11 HỌC247
-


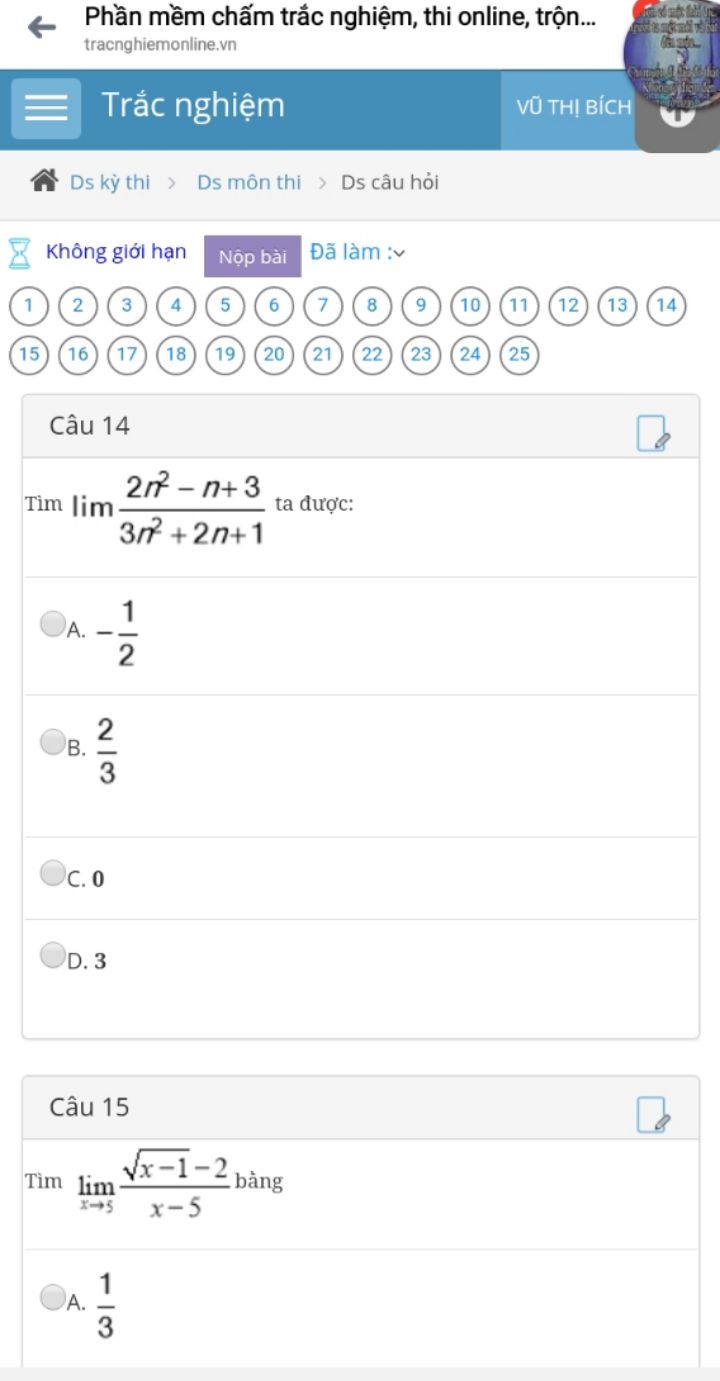
Tìm lim (2n^2-n+3)/(3n^2+2n+1)
bởi Nga Nguyễn
 22/02/2020
22/02/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


lim(x-->1)[((căn bậc 3)x^2)-(2.(căn bậc 3)x)+1]/(x-1)^2
Theo dõi (0) 0 Trả lời -


Tính giới hạn lim (x-->+ vô cực) x.căn x/(2x^2-x+1)
bởi Vũ Thị Huệ
 21/02/2020
21/02/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Giải bài tập
Giải bài tập Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính a+2b biết 2 số thực a và b thỏa mãn lim ((4x^2-3x+1)/(2x+1)-ax-b)=0 khi x tiến tới + vô cực
bởi Thành Martin
 19/02/2020
19/02/2020
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


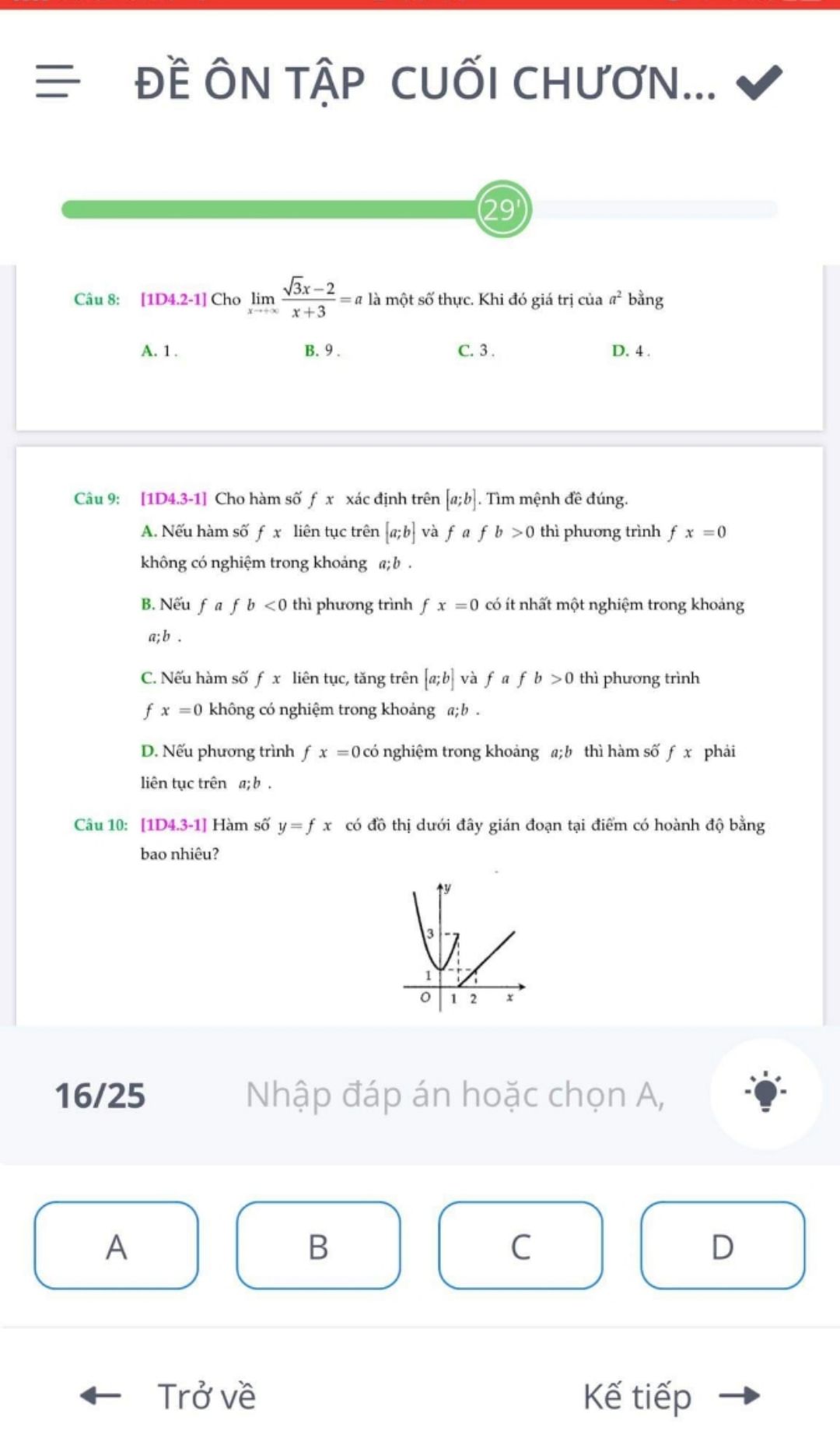
Tính giá trị của a^2 biết lim (căn 3x-2)/(x+3)=a khi x tiến tới + vô cực
bởi Thành Martin
 19/02/2020
19/02/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


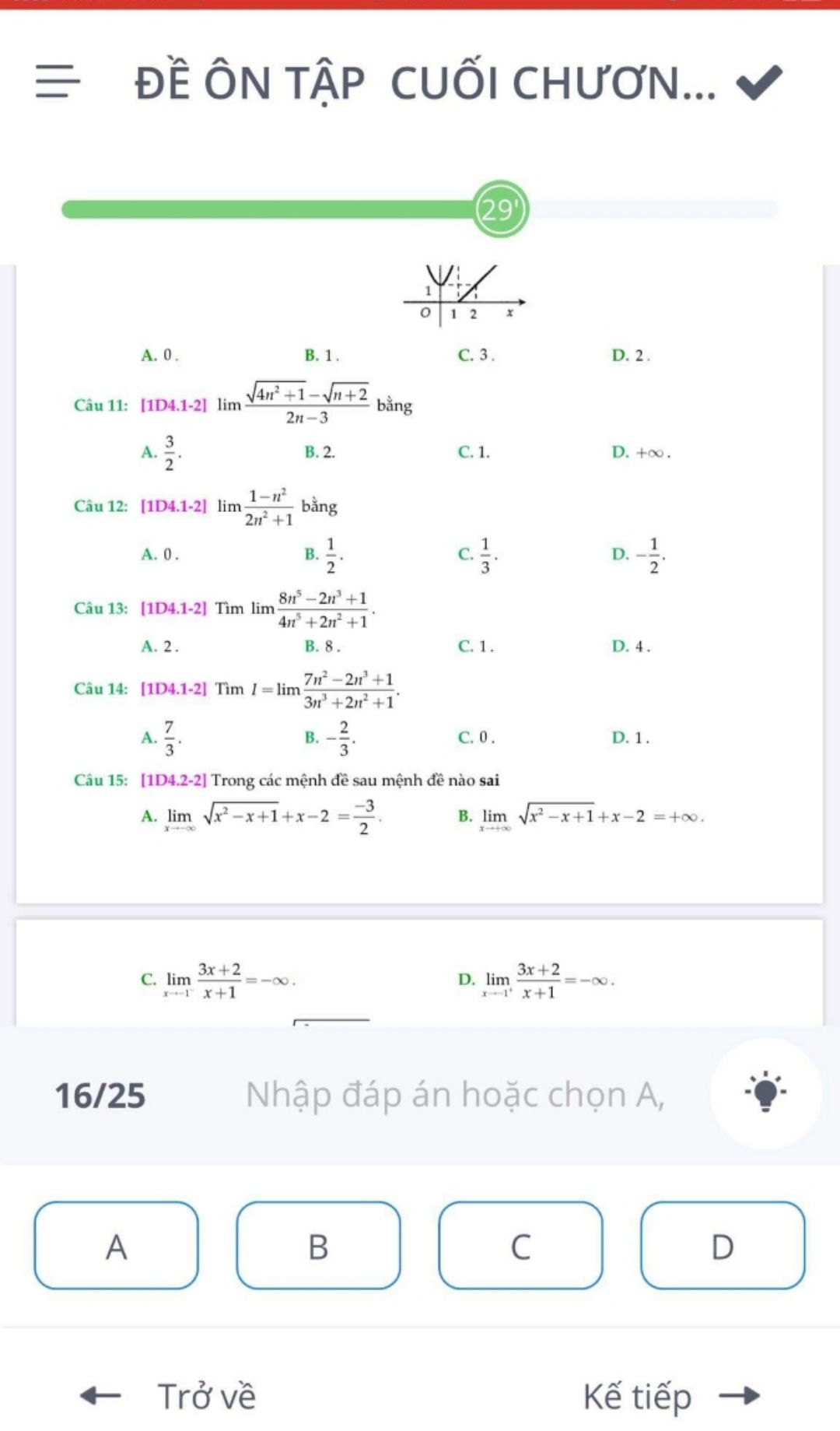
Tính lim (căn(4n^2+1)-căn(n+2))/(2n-3)
bởi Thành Martin
 19/02/2020
19/02/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 29 trang 159 SGK Toán 11 NC
Bài tập 30 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC





