Bài tập 25 trang 152 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - \infty } \sqrt[3]{{\frac{{{x^2} + 2x}}{{8{x^2} - x + 3}}}}\)
b) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt x }}{{{x^2} - x + 2}}\)
Hướng dẫn giải chi tiết
a)
\(\mathop {\lim }\limits_{x \to - \infty } \sqrt[3]{{\frac{{{x^2} + 2x}}{{8{x^2} - x + 3}}}} = \mathop {\lim }\limits_{x \to - \infty } \sqrt[3]{{\frac{{1 + \frac{2}{x}}}{{8 - \frac{1}{x} + \frac{3}{{{x^2}}}}}}} = \frac{1}{2}\)
b)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt x }}{{{x^2} - x + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt x }}{{{x^2}\left( {1 - \frac{1}{x} + \frac{2}{{{x^2}}}} \right)}}\\
= \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{\sqrt x \left( {1 - \frac{1}{x} + \frac{2}{{{x^2}}}} \right)}} = 0
\end{array}\)
(vì \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{\sqrt x }} = 0,\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{1 - \frac{1}{x} + \frac{2}{{{x^2}}}}} = 1\))
-- Mod Toán 11 HỌC247
-


Tính giới hạn của căn bậc 3(1 +x^2) -1 / x^2
bởi Lê Ngọc Bảo Châu
 30/03/2020
30/03/2020
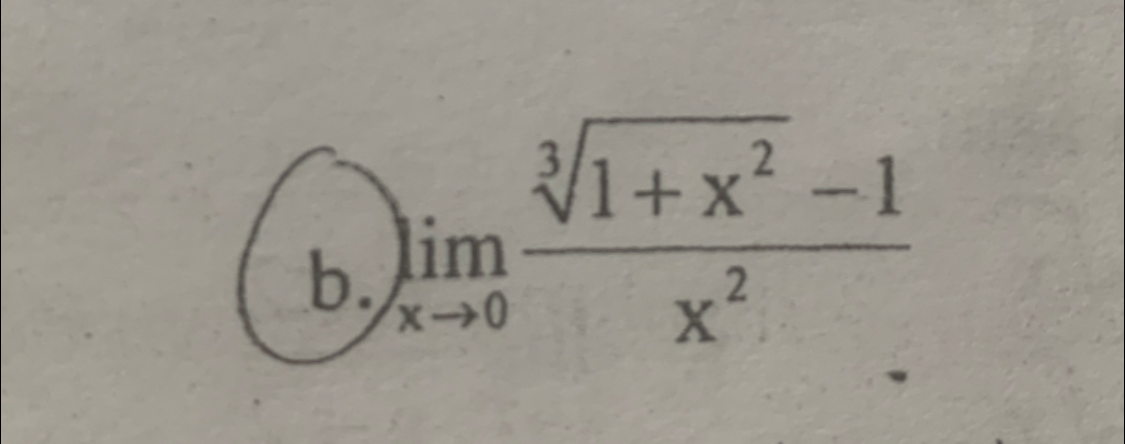 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính giới hạn tại âm vô cùng của hàm số căn(x^2-x+3)+x
bởi Vy Puka
 29/03/2020
29/03/2020
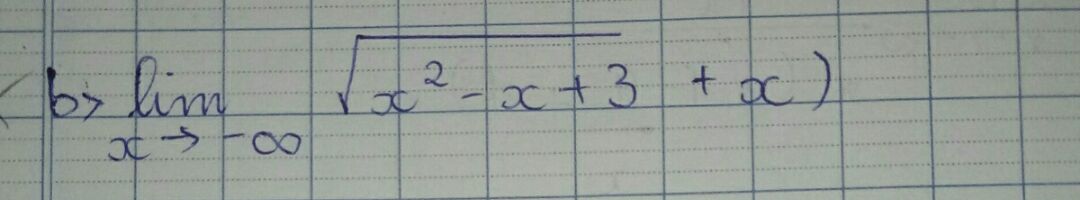 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính giới hạn tại x=0 của (sin 5x)/4x
bởi Vũ Thanh Nhàn
 28/03/2020
Làm giúp em câu B bài 1 với câu F bài 2 với ạ em cảm ơn
28/03/2020
Làm giúp em câu B bài 1 với câu F bài 2 với ạ em cảm ơn Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tính giới hạn tại +∞ của x^2-2x-3
bởi Ruly Thao
 25/03/2020
25/03/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời
Bài tập SGK khác
Bài tập 23 trang 152 SGK Toán 11 NC
Bài tập 24 trang 152 SGK Toán 11 NC
Bài tập 26 trang 158 SGK Toán 11 NC
Bài tập 27 trang 158 SGK Toán 11 NC
Bài tập 28 trang 158 SGK Toán 11 NC
Bài tập 29 trang 159 SGK Toán 11 NC
Bài tập 30 trang 159 SGK Toán 11 NC
Bài tập 31 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC





