Bài tập 36 trang 163 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^3} - 5}}{{{x^2} + 1}}\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^4} - x} }}{{1 - 2x}}\)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^3} - 5}}{{{x^2} + 1}} = \mathop {\lim }\limits_{x \to + \infty } x.\frac{{{x^2}\left( {1 - \frac{5}{{{x^3}}}} \right)}}{{\left( {1 + \frac{1}{{{x^2}}}} \right)}}\\
= \mathop {\lim }\limits_{x \to + \infty } x.\frac{{1 - \frac{5}{{{x^3}}}}}{{1 + \frac{1}{{{x^2}}}}} = + \infty
\end{array}\)
(vì \(\mathop {\lim }\limits_{x \to + \infty } x = + \infty ,\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - \frac{5}{{{x^3}}}}}{{1 + \frac{1}{{{x^2}}}}} = 1 > 0\))
b) Với mọi x < 0, ta có:
\(\frac{{\sqrt {{x^4} - x} }}{{1 - 2x}} = \frac{{{x^2}\sqrt {1 - \frac{1}{{{x^3}}}} }}{{1 - 2x}} = \frac{{\sqrt {1 - \frac{1}{{{x^3}}}} }}{{\frac{1}{{{x^2}}} - \frac{2}{x}}}\)
Vì \(\mathop {\lim }\limits_{x \to - \infty } \sqrt {1 - \frac{1}{{{x^3}}}} = 1,\mathop {\lim }\limits_{x \to - \infty } \left( {\frac{1}{{{x^2}}} - \frac{2}{x}} \right) = 0\) và \(\frac{1}{{{x^2}}} - \frac{2}{x} > 0\) với x < 0)
Do đó \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^4} - x} }}{{1 - 2x}} = + \infty \)
-- Mod Toán 11 HỌC247
-


Tìm a để lim(căn(x^2-3x+5)+ax)=- vô cực
bởi hii97
 10/01/2020
giúp mình với
10/01/2020
giúp mình với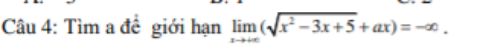 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -

 Help me please
Help me please Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính lim (x+1)/(x-1) khi x tiến tới 1-
bởi Zedd
 07/01/2020
07/01/2020
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tính giới hạn lim(căn x+căn(x+1)-1)/(x-1).(x^2+5x-7)
bởi Trân Kim
 31/03/2019
31/03/2019
Tính giới hạn sau đây
Theo dõi (1) 3 Trả lời -


Tính giới hạn lim x(x-3)/(x-căn(x+1)-1)
bởi Mai Trang
 25/10/2018
25/10/2018
\(\lim\limits_{x\rightarrow3}\dfrac{x\left(x-3\right)}{x-\sqrt{x+1}-1}\)
Theo dõi (0) 1 Trả lời -


Tính lim (2 căn x-3 căn(x+3)+2)/(x-1)
bởi Bo Bo
 25/10/2018
25/10/2018
lim\(\dfrac{2\sqrt{x}-3\sqrt{x+3}+2}{x-1}\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC






