Giải bài 4.9 tr 104 SBT Toán 10
Tìm giá trị nhỏ nhất của hàm số
\(y = \frac{4}{x} + \frac{9}{{1 - x}}\) với 0 < x < 1
Hướng dẫn giải chi tiết
\(\begin{array}{l}
y = \frac{{4\left( {x + 1 - x} \right)}}{x} + \frac{{9\left( {x + 1 - x} \right)}}{{1 - x}}\\
= 4 + 9 + \frac{{4\left( {1 - x} \right)}}{x} + 9.\frac{x}{{1 - x}} \ge 13 + 2\sqrt {4.\frac{{\left( {1 - x} \right)}}{x}.9.\frac{x}{{1 - x}}} = 25\\
\Rightarrow y \ge 25,\forall x \in \left( {0;1} \right)
\end{array}\)
Đẳng thức y = 25 xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}
\frac{{4\left( {1 - x} \right)}}{x} = \frac{{9x}}{{1 - x}} = 6\\
x \in \left( {0;1} \right)
\end{array} \right. \Leftrightarrow x = \frac{2}{5}\)
-- Mod Toán 10 HỌC247
-

 a^2 b^2 c^2>=2(ab bc-ac)Theo dõi (0) 0 Trả lời
a^2 b^2 c^2>=2(ab bc-ac)Theo dõi (0) 0 Trả lời -


Tìm GTLN của A= x^2(9-4x) với 0 < x < 9/4
bởi Time VR
 23/01/2020
23/01/2020
Tìm GTLN của A= x^2(9-4x) với 0<x<9/4 mong mn giúp mình
Theo dõi (0) 0 Trả lời -


Chứng minh a/b+c + b/c+a + c/a+b >= 3/2
bởi Thanh Thủy
 15/01/2020
15/01/2020
a/b+c + b/c+a + c/a+b >= 3/2
Theo dõi (1) 7 Trả lời -

 Ở trên ad ơiTheo dõi (0) 7 Trả lời
Ở trên ad ơiTheo dõi (0) 7 Trả lời -


Tìm min của hàm số y= 4(x-2)+1/2x với x > 0
bởi Nguyễn Đình Hưng
 13/01/2020
Tìm Min của hs y= 4(x-2) 1/2x với x>0
13/01/2020
Tìm Min của hs y= 4(x-2) 1/2x với x>0 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


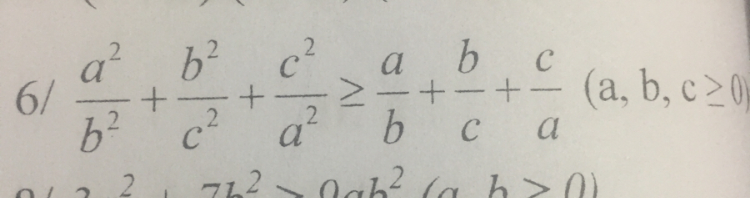 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Cho a,b,c>0. Chứng minh:
Theo dõi (0) 0 Trả lời -


Tìm min của f(x)=x+1/x^2, x > = 2
bởi Phạm Thành Lam
 06/01/2020
06/01/2020
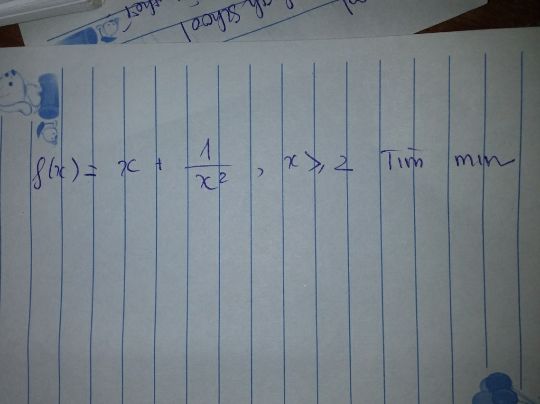 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Chứng minh a^2+b^2+ c^2 > = 1/3(a+ b +c)^2
bởi Tuyết Trinh
 05/01/2020
05/01/2020
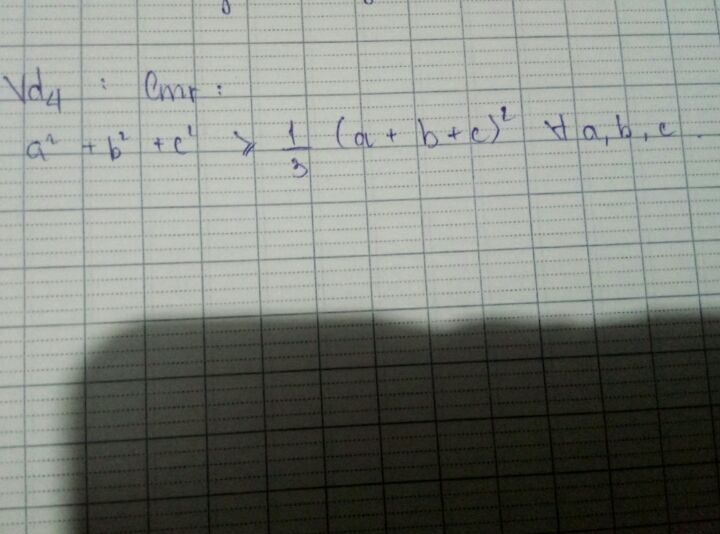 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4.7 trang 104 SBT Toán 10
Bài tập 4.8 trang 104 SBT Toán 10
Bài tập 4.10 trang 104 SBT Toán 10
Bài tập 4.11 trang 104 SBT Toán 10
Bài tập 4.12 trang 104 SBT Toán 10
Bài tập 4.13 trang 104 SBT Toán 10
Bài tập 4.14 trang 105 SBT Toán 10
Bài tập 4.15 trang 105 SBT Toán 10
Bài tập 4.17 trang 105 SBT Toán 10
Bài tập 4.16 trang 105 SBT Toán 10
Bài tập 4.18 trang 105 SBT Toán 10
Bài tập 2 trang 109 SGK Toán 10 NC
Bài tập 3 trang 109 SGK Toán 10 NC
Bài tập 4 trang 109 SGK Toán 10 NC
Bài tập 5 trang 110 SGK Toán 10 NC
Bài tập 6 trang 110 SGK Toán 10 NC
Bài tập 7 trang 110 SGK Toán 10 NC
Bài tập 8 trang 110 SGK Toán 10 NC
Bài tập 9 trang 110 SGK Toán 10 NC
Bài tập 10 trang 110 SGK Toán 10 NC
Bài tập 11 trang 110 SGK Toán 10 NC
Bài tập 12 trang 110 SGK Toán 10 NC
Bài tập 13 trang 110 SGK Toán 10 NC
Bài tập 14 trang 112 SGK Toán 10 NC
Bài tập 15 trang 112 SGK Toán 10 NC
Bài tập 16 trang 112 SGK Toán 10 NC
Bài tập 17 trang 112 SGK Toán 10 NC
Bài tập 18 trang 112 SGK Toán 10 NC





