Toán 12 Bài 2: Cực trị của hàm số

- Cho hàm số \(y=f(x)\) liên tục trên khoảng (a;b) và điểm \(x_0\in(a;b)\):

+ Hàm số \(f(x)\) đạt cực đại tại \(x_0\) nếu \(f(x_0)>f(x) \ \forall x\in (x_0-h,x_0+h) \setminus \left \{ x_0 \right \},h>0\)

+ Hàm số \(f(x)\) đạt cực tiểu tại x0 nếu \(f(x_0)0\).

a) Điều kiện cần để hàm số có cực trị

- \(f(x)\) đạt cực trị tại \(x_0\), có đạo hàm tại \(x_0\) thì \(f'(x_0)=0\).

b) Điều kiện đủ để hàm số có điểm cực đại và cực tiểu

- Điều kiện thứ nhất: Cho hàm số \(y=f(x)\) liên tục trên khoảng \(K = ({x_0} - h;{x_0} + h)\,(h > 0)\) và có đạo hàm trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\):

+ Nếu \(\left\{ \begin{array}{l}
f'(x) < 0\;\;\forall x \in \left( {{x_0} - h;x{}_0} \right)\\
f'(x) > 0\;\;\forall x \in \left( {x{}_0;{x_0} + h} \right)
\end{array} \right.\)  thì x₀ là điểm cực tiểu của hàm số \(f(x)\).

+  Nếu \(\left\{ {\begin{array}{*{20}{l}}
{f'(x) > 0\;\;\forall x \in \left( {{x_0} - h;{x_0}} \right)}\\
{f'(x) < 0\;\;\forall x \in \left( {{x_0};{x_0} + h} \right)}
\end{array}} \right.\) thì x₀ là điểm cực đại của hàm số \(f(x)\).

- Cách phát biểu khác dễ hiểu hơn: Đi từ trái sang phải

+ Nếu \(f(x)\) đổi dấu từ - sang + khi qua _{\(x_0\)} thì \(x_0\) là điểm cực tiểu.

+ Nếu \(f(x)\) đổi dấu từ + sang - khi qua \(x_0\) thì \(x_0\) là điểm cực đại.

- Điều kiện thứ hai: Cho hàm số \(y=f(x)\) có đạo hàm cấp hai trên khoảng \(K = ({x_0} - h;{x_0} + h)\,(h > 0)\):

+ Nếu \(f'(x_0)=0\), \(f''(x_0)<0\) thì \(x_0\) là điểm cực đại của hàm số \(f(x)\).

+ Nếu \(f'(x_0)=0\), \(f''(x_0)>0\) thì \(x_0\) là điểm cực tiểu của hàm số \(f(x)\).

a) Quy tắc 1

- Tìm tập xác định.

- Tính \(f'(x)\). Tìm các điểm tại đó\(f'(x)=0\) hoặc \(f'(x)\) không xác định.

- Lập bảng biến thiên.

- Từ bảng biến thiên suy ra các điểm cực đại, cực tiểu.

b) Quy tắc 2

- Tìm tập xác định.

- Tính \(f'(x)\). Tìm các nghiệm x_i của phương trình \(f'(x)=0\).

- Tính \(f''(x)\) và \(f''(x_i)\) suy ra tính chất cực trị của các điểm xi.

- Chú ý: nếu \(f''(x_i)=0\) thì ta phải dùng quy tắc 1 để xét cực trị tại xi.

Câu 1: Tìm các điểm cực đại, cực tiểu của các hàm số sau:

a) \(y = \frac{1}{3}{x^3} - {x^2} - 3x + \frac{4}{3}\)

b) \(y = \left| x \right|\left( {x + 2} \right)\)

Lời giải:

a) \(y = \frac{1}{3}{x^3} - {x^2} - 3x + \frac{4}{3}\)

Cách 1:

Hàm số có TXĐ: \(D=\mathbb{R}\)

\(y' = {x^2} - 2x - 3\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 3 \end{array} \right.\)

Bảng biến thiên: 

​

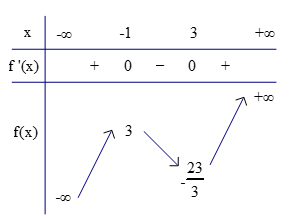
Kết luận:

Hàm số đạt cực đại tại \(x=-1\), giá trị cực đại tương ứng là \(y(-1)=3\);

Hàm số đạt cực tiểu tại \(x=3\), giá trị cực tiểu tương ứng là \(y_{CD}=-\frac{23}{3}\).

Cách 2: 

Hàm số có TXĐ: \(D=\mathbb{R}\)

\(y' = {x^2} - 2x - 3\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 3 \end{array} \right.\)

\(y ''= 2x - 2\)

 \(y''\left( { - 1} \right) = - 4 < 0\) suy ra hàm số đạt cực đại tại \(x=-1\), giá trị cực đại tương ứng là \(y(-1)=3\).

​\(y''\left( 3 \right) = 4 > 0\) suy ra hàm số đạt cực tiểu tại \(x=3\), giá trị cực tiểu tương ứng là \(y_{CD}=-\frac{23}{3}\).

b) \(y = \left| x \right|\left( {x + 2} \right)\)

Hàm số có TXĐ: \(D=\mathbb{R}\)

\(y' = \frac{x}{{\left| x \right|}}\left( {x + 2} \right) + \left| x \right| = \frac{{2\left( {{x^2} + x} \right)}}{{\left| x \right|}} (x\ne0)\)

Bảng biến thiên:

Kết luận:

Hàm số đạt cực đại tại \(x=-1,\) giá trị cực đại tương ứng là \(y(-1)=1;\) 

Hàm số đạt cực tiểu tại \(x=0,\) giá trị cực tiểu \(y(0)=0.\)

Câu 2: Tìm các điểm cực đại, cực tiểu của hàm số \(y=x-sin2x+2.\)

Lời giải: 

Hàm số có TXĐ: \(D=\mathbb{R}\)

\(y' = 1 - 2\cos 2x\)

\(y'=0 \Leftrightarrow \cos2x\Leftrightarrow x = \pm \frac{\pi }{6} + k\pi (k\in\mathbb{Z})\)

​\(y'' = 4\sin 2x\)

\(y''\left( {\frac{\pi }{6} + k\pi } \right) = 4\sin \left( {\frac{\pi }{3} + 2k\pi } \right) = 2\sqrt 3 > 0\) suy ra hàm số đạt cực tiểu tại \(x = \frac{\pi }{6} + k\pi\), giá trị cực tiểu tương ứng là \(y\left( {\frac{\pi }{6} + k\pi } \right) = {\textstyle{\pi \over 6}} + k\pi - \frac{{\sqrt 3 }}{2} + 2\).

​\(y''\left( { - \frac{\pi }{6} + k\pi } \right) = 4\sin \left( { - \frac{\pi }{3} + 2k\pi } \right) = - 2\sqrt 3 < 0\) suy ra hàm số đạt cực đại tại \(x = -\frac{\pi }{6} + k\pi\), giá trị cực đại tương ứng là \(y\left( { - \frac{\pi }{6} + k\pi } \right) = - \frac{\pi }{6} + k\pi - \frac{{\sqrt 3 }}{2} + 2\).​

Ví dụ 3: 

Tìm m để hàm số \(y = \left( {m + 2} \right){x^3} + 3{x^2} + mx - 5\) có 2 cực trị

Lời giải:

Với m=-2 hàm số trở thành \(y = 3{x^2} - 2x - 5\) không thể có hai cực trị. (1)

Với \(m\ne-2\) ta có: \(y' = 3\left( {m + 2} \right){x^2} + 6x + m\)

Hàm số có hai cực trị khi và chỉ khi phương trình \(y'=0\) có hai nghiệm phân biệt.

Điều này xảy ra khi: \(\Delta ' = - 3\left( {{m^2} + 2m - 3} \right) > 0 \Leftrightarrow {m^2} + 2m - 3 < 0 \Leftrightarrow - 3 < m < 1.\) (2)

Từ (1) (2) suy ra hàm số có hai cực trị khi: \(m \in \left( { - 3; - 2} \right) \cup \left( { - 2;1} \right)\)

Ví dụ 4: 

Tìm tất cả các giá trị thực của tham số m để hàm số \(\: y = -x^3 + (m+3)x^2 - (m^2 + 2m)x - 2\) đạt cực đại tại \(x=2.\)

Lời giải: 

Hàm số có tập xác định: \(D=\mathbb{R}\).

\(y' = -3x^2 + 2(m+3)x-(m^2 + 2m);\)

Để hàm số có cực trị tại \(x=2\) thì:

​\(y'(2) = 0 \Leftrightarrow - 12 + 4(m + 3) - {m^2} - 2m = 0 \Leftrightarrow \left[ \begin{array}{l} m = 0\\ m = 2 \end{array} \right.\)

Ta có: \(y'' = - 6x + 2(m + 3)\)

Với \(m=0\) thì \(y''(2)=-6<0.\)

Với \(m=2\) thì \(y''(2)=-2<0\).

Thứ lại với \(m=0\) và \(m=2\) hàm số đều đạt cực đại tại x=2.

Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 12 Chương 1 Bài 2 Cực trị của hàm số để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Hàm số y = f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây là đúng?

  

  • A. Hàm số đã cho có đúng một cực trị.
  • B. Hàm số đã cho không có giá trị cực đại.  
  • C. Hàm số đã cho có hai điểm cực trị.
  • D. Hàm số đã cho không có giá trị cực tiểu.

• Câu 2:

  Gọi A và B là hai điểm cực trị của đồ thị hàm số \(f\left( x \right) = {x^3} - 3x + 1.\) Tính độ dài AB.

  • A. \(AB = 2\sqrt 2\)
  • B. \(AB = 4\sqrt 2\)
  • C. \(AB = \sqrt 2\)
  • D. \(AB = \frac{\sqrt 2}{2}\)

• Câu 3:

  Tìm tất cả các giá trị thực của tham số m để hàm số \(y = - 2{x^4} + \left( {m + 3} \right){x^2} + 5\) có duy nhất một điểm cực trị.

  • A. \(m = 0\)
  • B. \(m \le - 3\)
  • C. \(m <3\)
  • D. \(m >-3\)

Câu 4 - 10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 12 Chương 1 Bài 2 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Giải tích 12 Cơ bản và Nâng cao.

Bài tập 1 trang 18 SGK Giải tích 12

Bài tập 2 trang 18 SGK Giải tích 12

Bài tập 3 trang 18 SGK Giải tích 12

Bài tập 4 trang 18 SGK Giải tích 12

Bài tập 5 trang 18 SGK Giải tích 12

Bài tập 6 trang 18 SGK Giải tích 12

Bài tập 1.17 trang 15 SBT Toán 12

Bài tập 1.18 trang 15 SBT Toán 12

Bài tập 1.19 trang 16 SBT Toán 12

Bài tập 1.20 trang 16 SBT Toán 12

Bài tập 1.21 trang 16 SBT Toán 12

Bài tập 1.22 trang 16 SBT Toán 12

Bài tập 1.24 trang 16 SBT Toán 12

Bài tập 1.23 trang 16 SBT Toán 12

Bài tập 1.25 trang 16 SBT Toán 12

Bài tập 1.26 trang 16 SBT Toán 12

Bài tập 1.27 trang 17 SBT Toán 12

Bài tập 1.28 trang 17 SBT Toán 12

Bài tập 1.29 trang 17 SBT Toán 12

Bài tập 1.30 trang 17 SBT Toán 12

Bài tập 1.31 trang 17 SBT Toán 12

Bài tập 1.32 trang 17 SBT Toán 12

Bài tập 1.33 trang 17 SBT Toán 12

Bài tập 11 trang 16 SGK Toán 12 NC

Bài tập 12 trang 17 SGK Toán 12 NC

Bài tập 13 trang 17 SGK Toán 12 NC

Bài tập 14 trang 17 SGK Toán 12 NC

Bài tập 15 trang 17 SGK Toán 12 NC

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, Hoc247 sẽ sớm trả lời cho các em.