Giải bài 3.38 tr 130 SBT Hình học 12
Tính khoảng cách giữa các cặp đường thẳng Δ và Δ′ trong các trường hợp sau:
a) \({\rm{\Delta }}:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + t}\\
{y = - 1 - t}\\
{z = 1}
\end{array}} \right.\) và \({\rm{\Delta '}}:\left\{ {\begin{array}{*{20}{c}}
{x = 2 - 3t'}\\
{y = 2 + 3t'}\\
{z = 3t'}
\end{array}} \right.\)
b) \(\Delta :\left\{ \begin{array}{l}
x = t\\
y = 4 - t\\
z = - 1 + 2t
\end{array} \right.\) và \({\rm{\Delta '}}:\left\{ {\begin{array}{*{20}{c}}
{x = t'}\\
{y = 2 - 3t'}\\
{z = - 3t'}
\end{array}} \right.\)
Hướng dẫn giải chi tiết
a) Gọi \((\alpha )\) là mặt phẳng chứa Δ và song song với Δ′. Hai vecto có giá song song hoặc nằm trên \((\alpha )\) là: \(\vec a = (1; - 1;0)\) và \({\vec a^\prime } = ( - 1;1;1)\). Suy ra \(\overrightarrow {{n_\alpha }} = ( - 1; - 1;0)\)
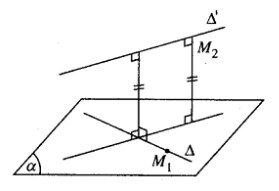
\((\alpha )\) đi qua điểm M1(1; -1; 1) thuộc Δ và có vecto pháp tuyến: \(\overrightarrow {{n_{\alpha '}}} = (1;1;0)\)
Vậy phưong trình của mặt phẳng \((\alpha )\) có dạng x – 1 + y + 1= 0 hay x + y = 0
Ta có: M2 (2; 2; 0) thuộc đường thẳng Δ′.
\(d({\rm{\Delta }},{\rm{\Delta '}}) = d({M_2},(\alpha )) = \frac{{|2 + 2|}}{{\sqrt {1 + 1} }} = 2\sqrt 2 \)
b) Hai đường thẳng Δ và Δ′ có phương trình là:
\(\Delta :\left\{ \begin{array}{l}
x = t\\
y = 4 - t\\
z = - 1 + 2t
\end{array} \right.\) và \({\rm{\Delta '}}:\left\{ {\begin{array}{*{20}{c}}
{x = t'}\\
{y = 2 - 3t'}\\
{z = - 3t'}
\end{array}} \right.\)
Phương trình mặt phẳng \((\alpha )\) chứa Δ và song song với Δ′ là 9x + 5y – 2z – 22 = 0
Lấy điểm M’(0; 2; 0) trên Δ′.
Ta có \(d({\rm{\Delta }},{\rm{\Delta '}}) = d(M',(\alpha )) = \frac{{|5.(2) - 22|}}{{\sqrt {81 + 25 + 4} }} = \frac{{12}}{{\sqrt {110} }}\)
Vậy khoảng cách giữa hai đường thẳng Δ và Δ′ là \(\frac{{12}}{{\sqrt {110} }}\).
-- Mod Toán 12 HỌC247
-


Trong không gian \(Oxyz\) cho điểm \({M_0}\left( {1;2;3} \right)\) và hai điểm \(M_1\left( {1 + t;2 + t;3 + t} \right)\), \({M_2}\left( {1 + 2t;2 + 2t;3 + 2t} \right)\) di động với tham số \(t\). Chứng tỏ ba điểm \({M_0},{M_1},{M_2}\) luôn thẳng hàng.
bởi Nguyen Dat
 06/05/2021
06/05/2021
Trong không gian \(Oxyz\) cho điểm \({M_0}\left( {1;2;3} \right)\) và hai điểm \(M_1\left( {1 + t;2 + t;3 + t} \right)\), \({M_2}\left( {1 + 2t;2 + 2t;3 + 2t} \right)\) di động với tham số \(t\). Chứng tỏ ba điểm \({M_0},{M_1},{M_2}\) luôn thẳng hàng.
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ trục tọa độ Oxyz. Cho mặt phẳng (P): x + 2y = 0. Đường thẳng d đi qua A(-1;3;-4) cắt Ox và song song với (P). Tìm một VTPT của đường thẳng d.
bởi Nguyễn Kim Ngân
 23/03/2021
23/03/2021
Câu 1: Trong không gian với hệ trục tọa độ Oxyz. Cho mặt phẳng (P): x + 2y = 0. Đường thẳng d đi qua A(-1;3;-4) cắt Ox và song song với (P). Tìm một VTPT của đường thẳng d.
A. (6;3;4).
B. (6;-3;-4).
C. (-6;3;4).
D. (6;-3;4).
Cảm ơn vì bạn đã trả lời.
Theo dõi (0) 4 Trả lời -


Trong không gian Oxyz cho A(124) B(312) C(311) D(-12-3). a. Viết phương trình mặt phẳng ABC. b. Tính khoảng cách từ d đến mặt phẳng ABC.
bởi Bảo Thanh
 21/03/2021
Trong không gian Oxyz cho A(124) B(312) C(311) D(-12-3).a. Viết phương trình mặt phẳng ABC.b. Tính khoảng cách từ d đến mặt phẳng ABC.c.Viết phương trình mặt phẳng chứa AB và song song CD. d. Viết phương trình mặt phẳng trung trực của đoạn AB.e.Gọi m n p lần lượt là hình chiếu của A lên Ox Oy Oz viết phương trình mặt phẳng (mnp).Theo dõi (0) 1 Trả lời
21/03/2021
Trong không gian Oxyz cho A(124) B(312) C(311) D(-12-3).a. Viết phương trình mặt phẳng ABC.b. Tính khoảng cách từ d đến mặt phẳng ABC.c.Viết phương trình mặt phẳng chứa AB và song song CD. d. Viết phương trình mặt phẳng trung trực của đoạn AB.e.Gọi m n p lần lượt là hình chiếu của A lên Ox Oy Oz viết phương trình mặt phẳng (mnp).Theo dõi (0) 1 Trả lời -


Trong không gian với hệ toạ độ Oxyz viết phương trình đường thẳng penta qua A(1,1,2) và vuông góc với d: x-1/2=y-2/1=z/2 đồng thời tạo với trục Oz góc lớn nhất.
bởi Trần Trà My
 07/03/2021
Giải giùm mình với ạTheo dõi (0) 0 Trả lời
07/03/2021
Giải giùm mình với ạTheo dõi (0) 0 Trả lời -


 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Trong ko gian oxyz cho A(2;3;-1), B(1;2;4), phương trình đường thẳng d đi qua hai điểm A,B là
bởi Ngọc Khánh
 01/03/2021
01/03/2021
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3.36 trang 130 SBT Hình học 12
Bài tập 3.37 trang 130 SBT Hình học 12
Bài tập 3.39 trang 130 SBT Hình học 12
Bài tập 3.40 trang 130 SBT Hình học 12
Bài tập 3.42 trang 131 SBT Hình học 12
Bài tập 3.43 trang 131 SBT Hình học 12
Bài tập 3.44 trang 131 SBT Hình học 12
Bài tập 3.45 trang 131 SBT Hình học 12
Bài tập 24 trang 102 SGK Hình học 12 NC
Bài tập 25 trang 102 SGK Hình học 12 NC
Bài tập 26 trang 102 SGK Hình học 12 NC
Bài tập 27 trang 103 SGK Hình học 12 NC
Bài tập 28 trang 103 SGK Hình học 12 NC
Bài tập 29 trang 103 SGK Hình học 12 NC
Bài tập 30 trang 103 SGK Hình học 12 NC
Bài tập 31 trang 103 SGK Hình học 12 NC
Bài tập 32 trang 104 SGK Hình học 12 NC
Bài tập 33 trang 104 SGK Hình học 12 NC





