Giải bài 3.45 tr 131 SBT Hình học 12
Cho hai đường thẳng d1: \(\frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 3}} = \frac{{z - 5}}{4}\) và d2: \(\left\{ {\begin{array}{*{20}{c}}
{x = 7 + 3t}\\
{y = 2 + 2t}\\
{z = 1 - 2t}
\end{array}} \right.\)
a) Chứng minh rằng d1 và d2 cùng nằm trong một mặt phẳng\((\alpha )\).
b) Viết phương trình của \((\alpha )\).
Hướng dẫn giải chi tiết
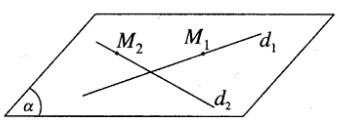
a) Ta có \(\overrightarrow {{a_{{d_1}}}} = (2; - 3;4)\) và \(\overrightarrow {{a_{{d_2}}}} = (3;2; - 2)\)
\(\vec n = \overrightarrow {{a_{{d_1}}}} \wedge \overrightarrow {{a_{{d_2}}}} = ( - 2;16;13)\)
Lấy điểm M1(1; -2; 5) trên d1 và điểm M2(7;2;1) trên d2.
Ta có \(\overrightarrow {{M_1}{M_2}} = (6;4; - 4)\)
\(\vec n.\overrightarrow {{M_1}{M_2}} = - 12 + 64 - 52 = 0\)
Suy ra d1 và d2 cùng nằm trong mặt phẳng \((\alpha )\).
b) Mặt phẳng \((\alpha )\) chứa M1 và có vecto pháp tuyến là \(\vec n\), vậy phương trình của \((\alpha )\) là:
\(-2(x-1) + 16(y + 2) + 13(z-5) = 0\) hay 2x – 16y – 13z + 31 = 0.
-- Mod Toán 12 HỌC247
-
Viết phương trình mặt phẳng (P) chứa đường thẳng d biết khoảng cách từ A(-1;2;3) đến (P) bằng 3
bởi Lê Tấn Thanh
07/02/2017
Khó quá, em bỏ cuộc rồi, mọi người giúp vs! Em cảm ơn nhiều ạ.
Viết phương trình mặt phẳng (P) chứa đường thẳng \(d:\left\{\begin{matrix} x=t\\ y=-1+2t\\ z=1 \end{matrix}\right.\) và khoảng cách từ A(-1;2;3) đến (P) bằng 3.
Theo dõi (0) 1 Trả lời -
Tìm tọa độ M' đối xứng với M qua \(\Delta\)
bởi Chai Chai
07/02/2017
Mình giải ra đáp số rồi mà không biết đúng hay sai nữa, khó quá.
Cho \(M(2;3;1), \Delta: \frac{x-2}{1}=\frac{y}{2}=\frac{z+1}{2}\). Tìm tọa độ M' đối xứng với M qua \(\Delta\)
Theo dõi (0) 1 Trả lời -
Viết phương trình đường thẳng \(\Delta\) đi qua M(3;-1;1), nằm trong mặt phẳng (P)
bởi can tu
06/02/2017
Em sẽ rất biết ơn ai giải giúp em bài này!
Viết phương trình đường thẳng \(\Delta\) đi qua M(3;-1;1), nằm trong mặt phẳng \((P):x-y+z-5=0\) và tạo với đường thẳng \(\Delta _1:\frac{x}{1}=\frac{y-2}{2}=\frac{z}{2}\) góc 450
Theo dõi (0) 4 Trả lời
